Laiko eilutės interpoliacija ir jos metodų taikymas atliekant finansinę analizę
Habil. dr. Jonas Mackevičius
Vilniaus universitetas,
Lietuva
el. paštas: jonas.mackevicius@evaf.vu.lt
ORCID: https://orcid.org/0000-0002-3350-6214
Dr.
Romualdas Valkauskas
Vilniaus universitetas, Lietuva
el.
paštas: romualdas.valkauskas@evaf.vu.lt
Dokt. Diana Bachtijeva
Vilniaus universitetas,
Lietuva
el. paštas: diana.bachtijeva@evaf.vu.lt
ORCID: https://orcid.org/0000-0003-3025-9841
Anotacija. Šiuolaikinėmis rinkos ekonomikos sąlygomis įmonių finansinei būklei ir veiklos rezultatams įvertinti svarbią reikšmę turi finansinės analizės informacija. Jos atlikimo metu naudojami bendri ekonominiai, matematiniai, euristiniai būdai. Straipsnyje nagrinėjama vieno iš matematinių tyrimo būdų – laiko eilutės būdo ir jos tyrimo metodų taikymo galimybės finansinėje analizėje, aptariama interpoliacijos metodų vieta ir vaidmuo finansinėje analizėje. Straipsnyje atskleista, kad interpoliacijos metodai, kurie gali būti naudojami siekiant nustatyti įmonės finansinių rodiklių buvusias reikšmes ar įvardinti priežastis, lėmusias įmonės finansinę būklę ir veiklos rezultatus yra šie: 1) grafiškoji bei aritmetinė interpoliacija tiesės lygtimi; 2) geometrinė interpoliacija pagal sudėtinių procentų formulę ir 3) interpoliacija vidurkiais.
Reikšminiai žodžiai: finansinė analizė, matematiniai tyrimo būdai, laiko eilutės būdas, interpoliacija, interpoliacijos metodai.
JEL klasifikacija: M49
Copyright
© 2020 Jonas Mackevičius, Romualdas Valkauskas, Diana Bachtijeva Published by Vilnius
University Press. This is an Open Access article distributed under the
terms of the Creative
Commons Attribution Licence, which permits unrestricted use,
distribution, and reproduction in any medium, provided the original author
and source are credited.
Pateikta / Submitted on
20.06.2020
Time series interpolation and application of its methods in financial analysis
Habil. dr. Jonas
Mackevičius
Vilnius University, Lithuania
Email: jonas.mackevicius@evaf.vu.lt
ORCID: https://orcid.org/0000-0002-3350-6214
Dr.
Romualdas Valkauskas
Vilnius University, Lithuania
Email: romualdas.valkauskas@evaf.vu.lt
PhD st. Diana Bachtijeva
Vilnius University,
Lithuania
Email: diana.bachtijeva@evaf.vu.lt
ORCID: https://orcid.org/0000-0003-3025-9841
Annotation. In the modern market economy conditions, financial information is very significant when evaluating the results of enterprises’ financial status and activity results. General economic, mathematical, heuristic methods are used for this type of analysis. The article analyses application opportunities for one of the mathematical research methods–time series–as well as its research instruments, discusses the place and role of interpolation methods in a financial analysis. The article reveals that interpolation methods which may be used to determined former values of an enterprise’s financial indicators or identify reasons which determined the enterprise’s financial status and activity results are the following: 1) graphic and arithmetic interpolation in a linear equation; 2) geometric interpolation based on the compound percentage formula and 3) interpolation by averaging.
Keywords: financial analysis, mathematical research methods, time series method, interpolation, interpolation methods.
JEL Code: M49
Copyright © 2020 Jonas
Mackevičius, Romualdas Valkauskas, Diana Bachtijeva
Published by Vilnius University
Press. This is an Open Access article distributed under the terms of the
Creative Commons
Attribution Licence, which permits unrestricted use, distribution, and
reproduction in any medium, provided the original author and source are
credited.
Pateikta / Submitted on
20.06.2020
Įvadas
Atliekant įmonių finansinę analizę taikomi bendri ekonominiai, matematiniai, loginiai, įvairūs kiti tyrimo būdai, kurie naudojami ir kituose moksluose: ekonomikos teorijoje, vadyboje, statistikoje, matematikoje ir kt. Šiais būdais, paimtą kiekvieną atskirai ar juos derinant ir formuojant analitines įmonės finansinės būklės ir veiklos rezultatų pažinimo sistemas, įvertinama finansinė būklė, turimų išteklių naudojimas ir panaudojimas, įvertinamas veiksnių poveikis įmonės veiklos rezultatams, prognozuojamos, modeliuojamos perspektyvos, tendencijų optimistiniai ir pesimistiniai variantai, įvertinami ir racionalizuojami galimi vadybos sprendimai įmonės veikos klausimais. Šiais būdais analizuojama įvairių rodiklių dinamika ir struktūra bei jos pokyčiai, įvertinami rodiklių tarpusavio ryšiai ir priklausomybė, nustatomi veiksniai ar jų grupės, turėjusios įtakos tam tikrų rodiklių ir jų sistemų pokyčiams. Literatūroje išsamiai aprašomi lyginimo, grupavimo, vidurkinių dydžių, indeksų, operacijų tyrimo, ekonometrijos, balansinių ryšių, koreliacinės analizės, regresinės analizės ir daugelis kitų būdų (Black, 2004; Palepu, Healy, Bernard, 2004; Savickaja (Савицкая, 2005); Lazauskas, 2005; Gronskas, 2006; Koroliov (Ковалёв, 2006); Mackevičius, 2007; Buškevičiūtė, Mačerinskienė, 2008; Mileris, 2009; Schlittgen, 2012; Tumelionis, 2013; Brag, 2013; Tamulevičienės, 2016; Ptak-Chmielewska, Kuleta, 2018; Stockemer, 2019 ir kt.).
Įmonių finansinėje analizėje matematinių būdų vieta savita. Tiesa, specialioje literatūroje, o ir praktikoje nėra vienareikšmių sprendinių, pagrindžiančių tų ar kitų matematinių būdų veiksmingumą ar naudingumą analizuojant įmonės finansinę būklę. Čia didesnio palankumo yra sulaukę statistikos bei ekonometrijos metodai. Aptariamas ir laiko eilutės būdas, nes finansinėje analizėje dažna praeities duomenų naudojimo praktika. Šis būdas efektyvus, jis padeda geriau suprasti įmonėje vykstančius procesus, nes norint pasakyti kas bus rytoj, reikia žinoti tai, kas įmonės viduje ar jos išorėje vyksta dabar, kokie procesai vyko praeityje. Tačiau, laiko eilutės būdui dėmesį skiria nedaugelis autorių (Mackevičius, 2007; Buškevičiūtė, Mačerinskienė, 2008; Giriūnas, Mackevičius, Valkauskas, 2014; Jiang ir kt., 2019; Cao, Li, 2019 ir kt.), apsiribodami bendromis laiko eilutės statistikos teorinėmis nuostatomis bei atsiribodami nuo to, kad būna ir taip, kai dalis, aprėžto laikotarpio ribomis, finansinio rodiklio duomenų yra nežinomi. Kitaip tariant, finansinės analizės praktikoje sutinkama “duomenų su tarpais” situacija. Laiko eilutės tyrimo efektyvumui svarbus tokių „tarpų“ užpildymo mechanizmas.
Tyrimo objektas – laiko eilutės interpoliacija.
Tyrimo tikslas – išnagrinėti laiko eilutės interpoliacijos esmę ir jos taikymo galimybes atliekant finansinę analizę.
Tyrimo tikslas apsprendžia šiuos pagrindinius tyrimo uždavinius:
1) išnagrinėti laiko eilutės interpoliacijos vietą matematinių tyrimo būdų sistemoje;
2) nustatyti laiko eilutės interpoliacijos metodus, kurie leistų objektyviau vertinti įmonės finansinę būklę ir veiklos rezultatus.
Tyrimo metodai – mokslinės literatūros analizės, informacijos grupavimo, lyginimo, detalizavimo ir apibendrinimo.
1. Ekstrapoliacija ir interpoliacija finansinės analizės tyrimo būdų sistemoje
Finansinėje analizėje taikant laiko eilučių būdą, laikoma,
kad yra žinomos reikšmės y(ti) i=1,2,...,n laiko momentais ir
visi stebėjimai atliekami vienodais laiko intervalais, t.y. ![]() (Stabingienė, 2015). Sudarant laiko eilutės modelį reikia įvertinti jos
stacionarumą, nes laiko eilutė yra stacionari, jei jos vidurkis, dispersija
ir autokovariacija išlieka ta pati nepriklausomai nuo to, kada jos
matuojamos. Tai bendri laiko eilutės statistikos teiginiai. Kita vertus,
įmonėje procesus, reiškinius ir veiksnius sieja įvairialypiai ryšiai. Jų
pobūdžio ir krypčių tyrinėjimas itin svarbus. Jis padeda atskleisti mažai
tikėtinas finansinės būklės ir veikos rezultatų gerinimo galimybes.
Finansinės analizės praktikoje taikant laiko eilutės būdą, analizuojant
laiko eilutes dažniausiai apsiribojama tam tikros laiko atkarpos
stebėjimais. Kitaip tariant, praeities duomenų analizės būdu bandoma
nusakyti dabartį ir nustatyti netikėtumą. Kitas tokių duomenų analizės
žingsnis – ateities numatymas – prognozavimas, kuris sprendžiamas
matematiniais finansinės analizės būdais vis dažniau tai „pavedant“
statistiniams laiko eilučių tyrimo metodams.
(Stabingienė, 2015). Sudarant laiko eilutės modelį reikia įvertinti jos
stacionarumą, nes laiko eilutė yra stacionari, jei jos vidurkis, dispersija
ir autokovariacija išlieka ta pati nepriklausomai nuo to, kada jos
matuojamos. Tai bendri laiko eilutės statistikos teiginiai. Kita vertus,
įmonėje procesus, reiškinius ir veiksnius sieja įvairialypiai ryšiai. Jų
pobūdžio ir krypčių tyrinėjimas itin svarbus. Jis padeda atskleisti mažai
tikėtinas finansinės būklės ir veikos rezultatų gerinimo galimybes.
Finansinės analizės praktikoje taikant laiko eilutės būdą, analizuojant
laiko eilutes dažniausiai apsiribojama tam tikros laiko atkarpos
stebėjimais. Kitaip tariant, praeities duomenų analizės būdu bandoma
nusakyti dabartį ir nustatyti netikėtumą. Kitas tokių duomenų analizės
žingsnis – ateities numatymas – prognozavimas, kuris sprendžiamas
matematiniais finansinės analizės būdais vis dažniau tai „pavedant“
statistiniams laiko eilučių tyrimo metodams.
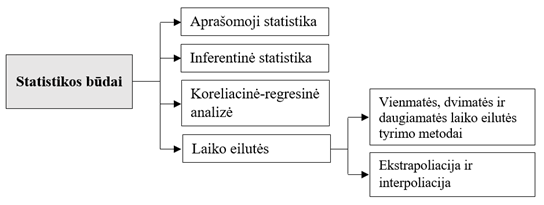
1 pav. Finansinės analizės statistikos būdai
Šaltinis: sudaryta autorių
1 paveiksle tarp laiko eilutės tyrimo metodų išskirti ekstrapoliacija ir interpoliacija. Apibendrintai analitinės praktikos – skaičiavimų patirtis tokia: analizuojant laiko eilutę išskiriama dėsningai kintanti dalis ir atsitiktinių priežasčių formuojama dalis. Dėsningai kintanti laiko eilutės dalis yra pavaldi matematiniam dėsniui ir todėl ji prognozuojama. Tokia sudėtinė dalis apskaičiuojama kiekvienam laiko momentui t kaip šio laiko momento t funkcija. Analizuojant parenkama matematinė kreivė, toliau įvertinama pasirinkimo paklaida bei nustatomas laiko eilutės dydis. Apskaičiavus matematinės funkcijos parametrų reikšmes sudaroma prognozė, t.y. atliekamas ekstrapoliacijos veiksmas. Ekstrapoliuojant nustatomos būsimos laiko eilutės reikšmės tiriamuoju laikotarpiu darant prielaidą, kad nustatytas dėsningumas išlieka ir už laiko eilutės ribų. Galima perspektyvinė ekstrapoliacija, kada atliekamas būsimų laiko eilutės reikšmių įvertinimus, arba retrospektyvinė ekstrapoliacija, kada atliekamas buvusių laiko eilutės reikšmių įvertinimus. Literatūroje šiuos klausimus plačiausiai tyrinėja Francis, 1993; Čekanavičius, Murauskas, 2000; Levine ir kt. 2005; Martišius, Kėdaitis, 2010.
Padėtis komplikuojasi, kai nėra žinomas finansinis rodiklis žinomo laikotarpio viduje, t.y. turime finansinio rodiklio laiko eilutę, kurioje yra „tarpų“ – yra nežinomų dėl tų ar kitų priežasčių rodiklių reikšmių (tarkime, nebuvo poreikio – reikalavimo skaičiuoti, nepavyko aptikti įmonės konkurentės vertinimams reikalingų to laikotarpio duomenų ir t.t.). Ne visais atvejais duomenys būna vienarūšiai ir kokybiški, duomenys yra tokios kokybės, kokios yra, jie turi „tarpų“.
“Tarpus” galima užpildyti pasitelkus statistikos teorijoje žinomą skaičiavimų techniką – būdus ar metodus, apibendrintai vadinamus interpoliacijos metodais. Pateiksime keletą statistikos ir ne statistikos literatūroje pateikiamų interpoliacijos apibrėžimų:
“Interpoliacija (lot. interpoliatio) – funkcijos tipinių reikšmių apytikslis nustatymas žinomomis jos reikšmėmis” (Tarptautinių žodžių žodynas, 1985, p. 217).
“… nežinomų laiko eilutės lygių nustatymas nagrinėjamo laikotarpio ribose vadinamas interpoliacija” (Aprašomoji statistika, 1998, p. 96).
“Analizuojant dinamiką, kartais atliekamas nežinomų dinamikos eilutės lygių įvertinimas nagrinėjamu laikotarpiu. Ši operacija vadinama interpoliacija” (Kunigėlytė, Laškovas, Markelevičius, 1986, p. 179).
“Sudarant ir analizuojant dinamikos eilutes, nežinomus jų lygius galima apytikriai apskaičiuoti. Kai nežinomas dinamikos eilutės lygis yra tarp dviejų žinomų lygių, jis randamas interpoliacijos būdu…” (Genienė, Čiulevičienė, 1998, p. 137, Čekanavičius, Murauskas, 2000).
Tai keletas interpoliacijos sąvokos paaiškinimų. Šį sąrašą būtų galima tęsti, tačiau tai komplikuoja viena aplinkybė, kurią pažymėjo dar akademikas A. Rimka (1939). Jis rašė: “Istoriškai aprašomosios statistikos vadovėliuose statistinės interpoliacijos metodai neliečiami ar neigiamai apibūdinami arba susiejami su statistinių eilučių išlyginimu bei pagrindinės linkmės nustatymu. Tačiau interpoliacijas sieti su išlyginimais formaliai tėra tiek pagrindo, kad interpoliacijoms kai kada naudojamas tos pačios tiesės bei parabolinės lygtys, taip pat aritmetinis, geometrinis, sumavimų ir kt. metodai, kurie ir statistikos eilučių ar linkmės nustatymams naudojami. O interpoliacijų statistinis uždavinys savaime yra kitas, ne kaip statistinio eilučių išlyginimo” (Rimka, 1939, p. 290 – 291). Šiandienos statistikos teorijos literatūroje padėtis pakitusi mažai ir nepaisant to, kad duomenų (ne tik įmonės finansinę padėtį identifikuojančių), naudojamų analitiniams vertinimams, tarpe vyraujantis „kraštinių skaičių“ atvejis. Analitikai susiduria su situacijomis, , kai tarp šių skaičių nėra ar nežinomi kiti skaičiai, tačiau spręsti klausimą ar interpoliacija yra statistiškai prasminga nėra šio tyrimo objektas, juolab, kad statistika ir duomenų “masiškumas” yra neatsiejami. Įmonės finansinėje analizėje svarbiau nustatyti ar laiko eilutės būdo interpoliacijos metodai gali padėti objektyviam įmonės finansinės būklės ir veiklos rezultatų vertinimui.
2. Finansinės analizės laiko eilutės būdo interpoliacijos metodai
Interpoliacija yra finansinės analizės laiko eilutės būdo komponentas, kuriuo naudojantis „panaikinami“, jeigu tokie yra, laiko eilutės tarpai. Šis komponentas didina laiko eilutės būdo veiksmingumą. Interpoliacijai gali būti naudojami statistikos, kitų mokslų metodai, finansinės analizės euristinis būdas ir kt. Itin veiksmingi statistikos metodai.
A. Francis (1993), Ch. Parker (2000), V. Čekanavičius, G. Murauskas (2000), K. Kardelis (2005), D. Levine, ir kt. (2005), V. Rudzkienė, M. Burinskienė (2007); S. Martišius, V. Kėdaitis (2010), R. Schlittgen (2012) ir daugelis kitų autorių išsamiai nagrinėja laiko eilučių tyrimo statistinius ekstrapoliacijos metodus, pateikia rekomendacijas jiems taikyti. Jie gali būti ir finansinės analizės laiko eilutės būdo interpoliacijos metodais. Galiausiai bent jau dėl to, kad analitikui nereikia pasikliauti viena iš euristikos hipotezių: sukauptas didelis kiekis racionaliai apdorotos informacijos (analitikas turi daug žinių ir patirties, gali remtis intuicija) ir vertinimas nesuformuos klaidingos ekonominių nuostolių atspalvio klaidos. Interpoliacija nepilnų duomenų atveju suteikia vertinimams didesnį pagrįstumą, o, tuo pačiu ir įmonės finansinės būklės ir veiklos rezultatų vertinimo didesnį objektyvumą.
Literatūroje taikomi skirtingi interpoliacijos metodai, priklausomai nuo to, kokio rezultato norima pasiekti (Meijering, 2002; Nareiko, Ruzgienė, Ūselis, 2010 ir kt.). Sekdami A. Rimka, kuris iš lietuvių autorių interpoliacijos klausimams skyrė daugiausiai dėmesio, remiantis jo įžvalgomis siūlome naudotinus finansinėje analizėje interpoliacijos metodus klasifikuoti kaip parodyta 2 paveiksle.
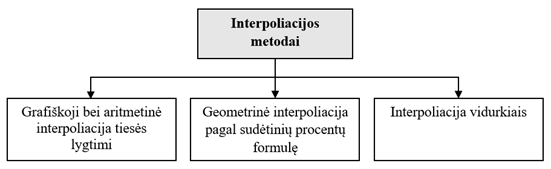
2 pav.
Interpoliacijos metodai
Šaltinis: sudaryta autorių
remiantis Rimka (1939)
2 paveiksle pateikti interpoliacijos metodai, kurie gali būti naudojami siekiant nustatyti įmonės finansinių rodiklių buvusias reikšmes ar įvardinti priežastis, lėmusias įmonės finansinę būklę ir veiklos rezultatus. Aptarsime šiuos metodus.
Grafiškoji bei
aritmetinė interpoliacija tiesės lygtimi yra paprasčiausias interpoliavimo
metodas. Jeigu dvi žinomas finansinio rodiklio reikšmes įstatysime į grafinę
koordinačių sistemą ir nubrėšime tiesę, tai ji rodys tas vietas, kurios yra
interpoliuojamos reikšmės. Geriausiai interpoliuojamoji reikšmė surandama iš
teisės lygties: ![]() ir jeigu šioje
lygtyje a yra pirma žinoma rodiklio skaitinė reikšmė (a =
y0), o b apskaičiuojama pagal formulę:
ir jeigu šioje
lygtyje a yra pirma žinoma rodiklio skaitinė reikšmė (a =
y0), o b apskaičiuojama pagal formulę:
![]()
čia: yn – antroji žinoma skaitinė reikšmė;
n – interpoliuojamų intervalų skaičius,
galima
sudaryti lygtį konkrečioms interpoliuojamoms reikšmėms apskaičiuoti ir jeigu
finansinio rodiklio žinomomis reikšmėmis yra y0 = 10 tūkst. eurų;
yn = 20 tūkst. eurų, n = 4, tai pagal šiuos duomenis turime: ![]() tūkst. eurų. Atsižvelgę į tai, turėsime šią
interpoliuojamiesiems skaičiams apskaičiuoti reikalingą formulę:
tūkst. eurų. Atsižvelgę į tai, turėsime šią
interpoliuojamiesiems skaičiams apskaičiuoti reikalingą formulę:
![]()
čia x – interpoliuojamo intervalo numeris,
Panaudojus šią formulę turėsime šias finansinio rodiklio reikšmes:
y0= 10 + (2,5![]() 0) = 10 tūkst.
eurų;
0) = 10 tūkst.
eurų;
y1= 10 + (2,5![]() 1) = 12,5 tūkst.
eurų;
1) = 12,5 tūkst.
eurų;
y2= 10 + (2,5![]() 2) = 15 tūkst.
eurų;
2) = 15 tūkst.
eurų;
y3= 10 + (2,5![]() 3) = 17,5 tūkst.
eurų;
3) = 17,5 tūkst.
eurų;
y4= 10 + (2,5![]() 4) = 20 tūkst.
eurų.
4) = 20 tūkst.
eurų.
Grafiškosios bei aritmetinės interpoliacijos tiesės lygtimi
metodas nėra be trūkumų. Gali būti taip, kad ![]() . Šiuo atveju
interpoliavimui naudojama lygtis turės tokį pavidalą:
. Šiuo atveju
interpoliavimui naudojama lygtis turės tokį pavidalą: ![]() . Be
to, “tarpas” tarp dviejų žinomų finansinio rodiklio reikšmių užpildomas
esant prielaidai, kad jame esantys skaičiai kinta aritmetine proporcija.
Gali būti taip, kad šie dydžiai kinta geometrine proporcija – vienodu
koeficientu. Tokiu atveju geriau naudoti geometrinės interpoliacijos pagal
sudėtinių procentų formulę metodą. Šiuo metodu skaičiuojant naudojama
formulė:
. Be
to, “tarpas” tarp dviejų žinomų finansinio rodiklio reikšmių užpildomas
esant prielaidai, kad jame esantys skaičiai kinta aritmetine proporcija.
Gali būti taip, kad šie dydžiai kinta geometrine proporcija – vienodu
koeficientu. Tokiu atveju geriau naudoti geometrinės interpoliacijos pagal
sudėtinių procentų formulę metodą. Šiuo metodu skaičiuojant naudojama
formulė:
![]()
čia 1 + p = 1 + i yra konstanta, nes p arba i yra palūkanų procentas. Finansinio rodiklio interpoliuojamų reikšmių atveju p = i = n . Tais atvejais, kai žinomos rodiklio reikšmės (y0) ir (yn), konstanta (koeficientas K) randama iš vidutiniam didėjimo tempui apskaičiuoti naudojamos formulės:
![]()
Aptarto
atvejo sąlygoms turime: ![]()
Tolesniais skaičiavimais gauname šias rodiklio skaitines reikšmes.
Kai n = 0
turime: 10 ![]() 1,189210 = 10 tūkst. eurų,
1,189210 = 10 tūkst. eurų,
kai n = 1 turime: 10 ![]() 1,189211 = 11,8921 tūkst. eurų,
1,189211 = 11,8921 tūkst. eurų,
kai n = 2
turime: 10 ![]() 1,189212 = 14,1422 tūkst. eurų,
1,189212 = 14,1422 tūkst. eurų,
kai n = 3 turime: 10 ![]() 1,189213 = 16,8181 tūkst. eurų,
1,189213 = 16,8181 tūkst. eurų,
kai n = 4
turime: 10 ![]() 1,189214 = 20,0002 tūkst. eurų.
1,189214 = 20,0002 tūkst. eurų.
Skaičiavimų rezultatai
artimi anksčiau pateiktiems. Tuomet, kai ![]() , interpoliuojamos
reikšmės yra atvirkštinėje proporcijoje. Geometrinė interpoliacija
prasminga, kai interpoliuotinų reikšmių skaičius n didesnis bei kai
y0 ir yn ženkliai skiriasi. Jei n mažas ir, be
to, y0 ir yn skirtumas nedidelis, skaičiavimuose
galima apsiriboti grafiškosios bei aritmetinė interpoliacijos tiesės lygtimi
metodu.
, interpoliuojamos
reikšmės yra atvirkštinėje proporcijoje. Geometrinė interpoliacija
prasminga, kai interpoliuotinų reikšmių skaičius n didesnis bei kai
y0 ir yn ženkliai skiriasi. Jei n mažas ir, be
to, y0 ir yn skirtumas nedidelis, skaičiavimuose
galima apsiriboti grafiškosios bei aritmetinė interpoliacijos tiesės lygtimi
metodu.
Interpoliacijos vidurkiais metodas naudojamas tuomet, kai
tarpe tarp žinomų rodiklio skaitinių reikšmių y0 ir yn
reikia apskaičiuoti vidurinę jo reikšmę. Šiuo atveju interpoliuojama
aritmetiniu arba geometriniu vidurkiu. Vidurkio formą lemia konkreti
situacija. Nagrinėjant plačiau, remėmės atveju, kai finansinio rodiklio
reikšmės sudarė: y0= 10 tūkst. eurų; yn= 20 tūkst.
eurų ir ėmėme n=4. Skaičiuojant tiesės lygtimi, interpoliuojamoji reikšmė
y2 buvo surasta taip: y2= 10 + 2,5 ![]() 2 =
15 tūkst. eurų, o skaičiuojant geometriniu metodu, ši reikšmė buvo
apskaičiuotas taip: 10
2 =
15 tūkst. eurų, o skaičiuojant geometriniu metodu, ši reikšmė buvo
apskaičiuotas taip: 10 ![]() 1,189212 = 14,1422 tūkst. eurų. Panašius skaičiavimų rezultatus
gauname ir interpoliuojant vidurkiais:
1,189212 = 14,1422 tūkst. eurų. Panašius skaičiavimų rezultatus
gauname ir interpoliuojant vidurkiais:
1) naudojant paprasto aritmetinio vidurkio formulę:
![]()
2) naudojant geometrinio vidurkio formulę turime:
![]()
Interpoliuojant vidurkiais galima naudoti ir kitas vidurkio formas: kvadratinį, harmoninį, antiharmoninį ir kt. Vidurkio formą lemia skaičiavimų turinys.
Taigi, kiekvienas metodas turi savitumų ir parenkant optimalų situacijai tikslinga remtis metodo pasikliautinumo galimybe, kuri gali būti vertinama šiais kriterijais:
1) įtikimumas– tai kriterijus, parodantis, kad naudojamu metodu apskaičiuota konkreti, laiko eilutėje „trūkstama“ finansinio rodiklio reikšmė tikroviška ir įtikinama;
2) patikimumas – parodo, ar skaičiavimų tvarka - metodika buvo nuosekli;
3) patvirtinamumas – parodo, ar skaičiavimų rezultatai yra neutralūs ir neįtakoti analitiko subjektyvių pozicijų, ar įmanoma pakartoti skaičiavimus ir jais pasiekti panašių rezultatų.
Patvirtinamumas gali būti užtikrintas ir skaičiavimų rezultatą – „užpildytą“ laiko eilutę detaliai vertinant, atitolstant nuo viso sukaupto žinojimo apie finansinį reiškinį ar situaciją, vertinant ar skaičiavimų rezultatas atitinka finansinės analizės laiko eilutės būdą ir tokia laiko eilutė tinka gilesnei analizei statistikos, kitų mokslų metodais.
Išvados
1. Finansinės analizės praktikoje taikant matematinius tyrimo būdus naudojamas ir laiko eilutės būdas, t.y. istorinių duomenų pagrindu bandoma nusakyti dabartį, numatyti ateitį (perspektyvinė ekstrapoliacija) arba atskleisti praeities ypatybes (retrospektyvinė ekstrapoliacija). Ekstrapoliuojant nustatomos būsimos laiko eilutės reikšmės tiriamuoju laikotarpiu darant prielaidą, kad nustatytas dėsningumas išlieka ir už laiko eilutės ribų. Padėtis sudėtingesnė, kai turime finansinio rodiklio laiko eilutę, kurioje yra „tarpų“ –nežinomų dėl tų ar kitų priežasčių rodiklio reikšmių. Ne visais atvejais duomenys būna vienarūšiai ir kokybiški. „Tarpus“ galima užpildyti pasitelkus statistikos teorijoje žinomą skaičiavimų techniką – būdus ar metodus, apibendrintai vadinamus interpoliacijos metodais. Šiais metodais apytikriai apskaičiuojamos nežinomos rodiklio laiko eilutės reikšmės.
Statistikos teorijos literatūroje reiškinių, procesų interpoliacija ir jos metodai tyrinėjami. Dėmesys sutelkiamas į ekstrapoliacijos metodus ar būdus, teigiant, kad jie gali būti ir interpoliacijos metodais. Neneigiant šio tvirtinimo, nereikėtų tapatinti ekstrapoliacijos ir interpoliacijos uždavinių. Jie turiniu skirtingi. Interpoliacijos keliu laiko eilute “sutvarkoma”, bet ne “išlyginama” jos pagrindinės vystymosi tendencijos nustatymo keliu. Finansinės analizės tyrimo būdų sistemoje laiko eilutės būdo papildymas interpoliaciniais skaičiavimais – problematiškų laiko eilučių “sutvarkymas” interpoliacijos metodais, didina įmonės finansinės būklės ir veiklos rezultatų vertinimo objektyvumą.
2. Interpoliacijos metodai, kurie gali būti naudojami siekiant nustatyti įmonės finansinių rodiklių buvusias reikšmes ar įvardinti priežastis, lėmusias įmonės finansinę būklę ir veiklos rezultatus yra šie: 1) grafiškoji bei aritmetinė interpoliacija tiesės lygtimi; 2) geometrinė interpoliacija pagal sudėtinių procentų formulę ir 3) interpoliacija vidurkiais. Kiekvienas metodas yra savitas ir parenkant optimalų, tikslinga remtis metodo pasikliautinumo galimybe, kuri gali būti vertinama įtikimumo, patikimumo ir patvirtinamumo kriterijais.
Literatūra
Aprašomoji statistika, 1998. Vilnius.: Vilniaus universiteto leidykla.
Black, G., 2004. Applied Financial Accounting and Reporting. Oxford University Press.
Brag, S., 2013. Financial Analysis. A Business Decision Guide. John Willey and Sons Ltd.
Buškevičiūtė, E.; Mačerinskienė, I., 2008. Finansų analizė. Kaunas: Technologija.
Cao J.; Li Z.; Li J., 2019. Financial time series forecasting model based on CEEMDAN and LSTM. Physica A: Statistical Mechanics and its Applications. Nr. 519, p. 127-139.
Čekanavičius, V.; Murauskas, G., 2000. Statistika ir jos taikymai. I dalis. Vilnius, TEV.
Francis, A., 1993. Business Mathematics and Statistics. London: DP Publications.
Genienė, M.; Čiulevičienė, V., 1998. Bendroji ir žemės ūkio statistika. Vilnius: Mintis.
Gronskas, V., 2006. Ekonominė analizė. Kaunas: Technologija.
Jiang Z. Q., ir kt., 2019. Multifractal analysis of financial markets: a review. Reports on Progress in Physics, Nr. 82. https://doi.org/10.1088/1361-6633/ab42fb
Kardelis, K., 2005. Mokslinių tyrimų metodologija ir metodai. Šiauliai: Lucilijus.
Kunigėlytė, L.; Laškovas, J.; Markelevičius, J., 1986. Bendroji statistikos teorija. Vilnius: Mintis.
Lazauskas, J., 2005. Įmonių ūkinės ir komercinės veiklos ekonominė analizė. Vilnius: Technika.
Levine, D. ir kt., 2005. Statistics for Managers using Microsoft. Pearson Education, Inc., Upper Saddle River, New Jersey.
Mackevičius, J., 2007. Įmonių veiklos analizė. Informacijos rinkimas, sisteminimas ir vertinimas. Vilnius: TEV.
Mackevičius, J.; Giriūnas, L.; Valkauskas, R., 2014. Finansinė analizė. Vilnius: Vilniaus universiteto leidykla.
Martišius, S.; Kėdaitis, V., 2010. Statistika. 1 dalis. Statistinės analizės teorija ir metodai. Vilnius: Vilniaus universiteto leidykla.
Meijering E. 2002. A chronology of interpoliation: from ancient astronomy to modern signal and image processing. Proccedings of the IEEE, T. 90, p. 319-342.
Mileris, R., 2009. Statistinių kredito rizikos vertinimo modelių efektyvumo analizė. Ekonomika ir vadyba. Nr. 14, p. 1156-1162, ISSN 1822-6515.
Nareiko, V.; Ruzgienė, B.; Ūselis, A., 2010. Deterministinių ir geostatistinių interpoliavimo metodų taikymas žemės paviršiui modeliuoti. Geodezija ir kartografija, Nr. 36(3), p. 118-122. https://doi.org/10.3846/gc.2010.19.
Palepu, K.; Healy, P.; Bernard, V., 2004. Business Analysis and Valuation. Using Financial Statements. Thomson, South-Western.
Parker, Ch., 2000. Performance measurement. Work Study, 49(2), 63-66.
Ptak-Chmielewska A.; Kuleta, P., 2018. Statistical models in enterprises default risk assessment–an example of application. Econometrics. Nr. 22(1), p. 94-106.
Rimka, A., 1939. Statistika. Teorija ir metodai. Kaunas: Spindulys.
Schlittgen, R., 2012. Einführung in die Statistik. Analyse und Modellierung von Daten. München, Wien:Oldenbourg.
Stabingienė, L., 2015. Ekonometrika. Kaunas, KU leidykla, ISBN: 978-9955-18-863-6.
Stockemer, D., 2019. Multivariate Regression Analysis. Quantitative Methods for the Social Sciences. p. 163-174. http://doi.org/10.1007/978-3-319-99118-4_9
Tamulevičienė, D., 2016. Methodology of complex analysis of companies’ profitability. Entrepreneurship and sustainability issues. 4(1), 53-63. http://doi.org/10.9770/jesi.2016.4.1(5).
Tarptautinių žodžių žodynas, 1985. Vilnius: Mokslas.
Tumelionis, A., 2013. Lyginamojo metodo pataisų apskaičiavimo aktualijos. Turto vertinimo teorijos ir praktikos apybraižos, p 38-54. ISSN 2335-2310.
Ковалёв, В., 2006. Финансовый анализ: методы и процедуры. Москва: Финансы и статистика.
Савицкая, В., 2005. Методика комплексного анализа хозяйственной деятельности. Москва: ИНФРА.
Habil. Dr. Jonas, Mackevičius: Vilniaus universiteto, ekonomikos ir verslo administravimo fakulteto, apskaitos ir audito katedros profesorius emeritas. Mokslinių interesų sritys – tarptautinė finansinė apskaita, auditas, valdymo apskaita, finansinė analizė. Vilniaus universitetas, Ekonomikos ir verslo administravimo fakultetas, Apskaitos ir audito katedra. Institucijos adresas: Saulėtekio al. 9, II rūmai, LT-10222, Vilnius.
Habil. Dr. Jonas, Mackevičius: Professor Emeritus of Accounting and Auditing Department, Faculty of Economics and Business Administration, Vilnius University. Scientific interests: international accounting, auditing, financial analysis, management accounting.
Dr. Romualdas, Valkauskas: socialinių mokslų daktaras (04S), docentas. Mokslinių interesų sritys – kiekybiniai metodai socialiniuose moksluose, taikomosios statistikos metodai, ekonominė statistika, statistikos teorijos ir praktikos istorija. Vilniaus universitetas, Ekonomikos ir verslo administravimo fakultetas, Kiekybinių metodų ir modeliavimo katedra. Institucijos adresas: Saulėtekio al. 9, II rūmai, LT-10222, Vilnius.
Dr. Romualdas, Valkauskas: assoc. Professor, Doctor of social sciences (04S). Scientific interests – quantitative methods in social sciences, applied statistical methods, economic statistics, history of theory and practice of statistics. Vilnius University, Faculty of Economics and Business Administration, department of Quantitative Method and Modelling. Address of institution: Saulėtekio av. 9, II building, LT-10222, Vilnius.
Diana Bachtijeva, Vilniaus universiteto, Ekonomikos ir verslo administravimo fakulteto, apskaitos ir audito katedros doktorantė. Mokslinių interesų sritys – kūrybinė apskaita, finansinė apskaita, finansinė analizė. Institucijos adresas: Saulėtekio al. 9, II rūmai, LT-10222, Vilnius.
Diana Bachtijeva, PHD candidate of Accounting and Auditing Department, Faculty of Economics and Business Administration, Vilnius University. Scientific interests: creative accounting, financial accounting, financial analysis. Address of institution: Saulėtekio av. 9, II building, LT-10222, Vilnius.