Dviejų lygių iteracinis tabu paieškos algoritmas kvadratinio paskirstymo uždaviniui
Alfonsas Misevičius
Kauno technologijos
universiteto
Multimedijos inžinerijos katedros tech. m. dr.,
profesorius
Kaunas University of Technology,
Department of
Multimedia Engineering, Dr., Prof.
Studentų g. 50-400/416a, LT-51368
Kaunas
El. paštas alfonsas.misevicius@ktu.lt
Dovilė
Kuznecovaitė (Verenė)
Kauno technologijos
universiteto
Multimedijos inžinerijos katedros doktorantė
Kaunas
University of Technology,
Department of Multimedia Engineering, PhD
Student
Studentų g. 50-408, LT-51368 Kaunas
El. paštas dovile.kuznecovaite@ktu.lt
Santrauka. Šiame straipsnyje nagrinėjamas vadinamasis dviejų lygių iteracinis tabu paieškos (ITP) algoritmas kvadratinio paskirstymo (KP) uždaviniui. Algoritmo naujumas yra tas, jog į jį yra integruotos sprendinių mutavimo procedūros, kurių esminė paskirtis yra diversifikuoti paieškos procesą, išvengiant paieškos stagnacijos ir taip padidinant jos efektyvumą. Algoritmo veikimas išbandytas su įvairių tipų mutavimo procedūrų realizavimo variantais. Atlikti kompiuteriniai eksperimentai su KP uždavinio testavimo duomenų pavyzdžiais iš standartinių pavyzdžių bibliotekos QAPLIB. Pateikti eksperimentų rezultatai, kurie iliustruoja, kaip skirtingos prigimties mutavimo procedūros, esančios ITP sudėtyje, gali įvairiai paveikti algoritmo efektyvumą.
Pagrindiniai žodžiai: skaitmeninis intelektas, kombinatorinis optimizavimas, euristiniai optimizavimo algoritmai, tabu paieška, mutavimo procedūros, kvadratinio paskirstymo uždavinys.
A 2-Level Iterated Tabu Search Algorithm for the Quadratic Assignment Problem
Summary. In this paper, a 2-level iterated tabu search (ITS) algorithm for the solution of the quadratic assignment problem (QAP) is considered. The novelty of the proposed ITS algorithm is that the solution mutation procedures are incorporated within the algorithm, which enable to diversify the search process and eliminate the search stagnation, thus increasing the algorithm’s efficiency. In the computational experiments, the algorithm is examined with various implemented variants of the mutation procedures using the QAP test (sample) instances from the library of the QAP instances – QAPLIB. The results of these experiments demonstrate how the different mutation procedures affect and possibly improve the overall performance of the ITS algorithm.
Keywords: computational intelligence, combinatorial optimization, heuristic algorithms, tabu search, mutation procedures, quadratic assignment problem.
Received: 25/10/2018. Accepted: 14 /2/2019
Copyright © 2018 Alfonsas Misevičius, Dovilė Kuznecovaitė (Verenė). Published by Vilnius University Press. This is an Open Access article distributed under the terms of the Creative Commons Attribution Licence, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Įvadas
Kvadratinio
paskirstymo (KP) uždavinys (angl. quadratic assignment problem
(QAP)) matematiškai formuluojamas taip. Duotos dvi neneigiamų
sveikųjų skaičių matricos ![]() ir
ir ![]() , taip pat aibė
, taip pat aibė ![]() , kurią sudaro
visi galimi natūrinių skaičių nuo
, kurią sudaro
visi galimi natūrinių skaičių nuo ![]() iki
iki ![]() perstatymai[1]. Tikslas yra surasti perstatymą
perstatymai[1]. Tikslas yra surasti perstatymą
![]() ir tokį, jog būtų minimizuota ši funkcija:
ir tokį, jog būtų minimizuota ši funkcija:
![]() . (1)
. (1)
Dėstymo teorijos
(angl. location theory) kontekste su KP uždaviniu gali būti
modeliuojamas ![]() įrengimų išdėstymas į
įrengimų išdėstymas į ![]() paskyrimo vietų, turint tikslą
minimizuoti bendrą kainą, atsižvelgiant į įrengimų susietumą ir atstumus
tarp paskyrimo vietų (Koopmans, Beckmann, 1957). Čia matricos
paskyrimo vietų, turint tikslą
minimizuoti bendrą kainą, atsižvelgiant į įrengimų susietumą ir atstumus
tarp paskyrimo vietų (Koopmans, Beckmann, 1957). Čia matricos ![]() reikšmės
asocijuojamos su įrengimų susietumo svoriais, o matricos
reikšmės
asocijuojamos su įrengimų susietumo svoriais, o matricos ![]() reikšmės nurodo
atstumus tarp paskyrimo vietų.
reikšmės nurodo
atstumus tarp paskyrimo vietų.
Dar vienas kvadratinio paskirstymo
uždavinio taikymo pavyzdys – tai elektroninių komponentų išdėstymas
spausdinto montažo plokštės (ar kristalo) pozicijose (Hanan, Kurtzberg,
1972). Šiame kontekste matricos ![]() elementai yra elektrinių
sujungimų tarp komponentų porų kiekiai. Matricos
elementai yra elektrinių
sujungimų tarp komponentų porų kiekiai. Matricos ![]() elementai atitinka atstumus
tarp fiksuotų pozicijų montažinėje plokštėje (kristale). Tuomet perstatymas
elementai atitinka atstumus
tarp fiksuotų pozicijų montažinėje plokštėje (kristale). Tuomet perstatymas
![]() gali būti interpretuojamas kaip atskira komponentų išdėstymo pozicijose
konfigūracija. Perstatymo elementas
gali būti interpretuojamas kaip atskira komponentų išdėstymo pozicijose
konfigūracija. Perstatymo elementas ![]() šiuo atveju nurodo numerį
pozicijos, į kurią paskirtas i-tasis komponentas. Tokiu būdu
šiuo atveju nurodo numerį
pozicijos, į kurią paskirtas i-tasis komponentas. Tokiu būdu ![]() (tiksliau,
(tiksliau, ![]() ) gali būti suprantamas kaip bendras sujungimų tarp komponentų
ilgis, kuomet visi
) gali būti suprantamas kaip bendras sujungimų tarp komponentų
ilgis, kuomet visi ![]() komponentai yra išdėstyti
atitinkamose
komponentai yra išdėstyti
atitinkamose ![]() pozicijų. (Literatūroje galima rasti ir dar daugiau KP
uždavinio praktinio taikymo pavyzdžių aprašymų (Çela, 1998).)
pozicijų. (Literatūroje galima rasti ir dar daugiau KP
uždavinio praktinio taikymo pavyzdžių aprašymų (Çela, 1998).)
Kita
vertus, KP uždavinys yra matematinis uždavinys, t. y. kombinatorinio
optimizavimo uždavinys. Šiuo atveju tikslas yra surasti optimalų sprendinį,
kur sprendiniai yra išreiškiami natūrinių skaičių perstatymais. Optimalumo
kriterijus aprašomas (1) formule, o funkcija ![]() yra vadinama tikslo funkcija
(TF).
yra vadinama tikslo funkcija
(TF).
Įrodyta, jog KP uždavinys priklauso NP sunkių optimizavimo
uždavinių klasei (Sahni, Gonzalez, 1976). Tai reiškia, kad skaičiavimų
laikas, reikalingas optimumui pasiekti, yra susietas su uždavinio apimtimi
![]() eksponentine priklausomybe. Dėl šios priežasties KP uždavinio sprendimui
naudojami euristiniai optimizavimo algoritmai (Michalewicz, Fogel, 2000;
Yang, 2010; Edelkamp, Schrödl, 2012; Siarry, 2016). Nors šie algoritmai
negarantuoja optimalaus sprendinio suradimo, tačiau jie leidžia gauti
pakankamai aukštos kokybės (artimus optimaliems) sprendinius per priimtiną
skaičiavimų laiką. KP uždaviniui sėkmingai išbandyti šie euristiniai
algoritmai: atkaitinimo modeliavimas (angl. simulated annealing)
(Misevičius, 2003), genetiniai algoritmai (angl. genetic algorithms)
(Merz, Freisleben, 2000; Drezner, 2003; Misevicius, 2004; Tang ir kt., 2006;
Ahmed, 2015; Benlic, Hao, 2015; Chmiel, Kwiecień, 2018), tabu paieška (angl.
tabu search) (Taillard, 1991; Misevicius, 2005; Shylo, 2017),
godžiosios randomizuotos adaptyvios paieškos procedūros (angl. greedy
randomized adaptive search procedures (GRASP)) (Li ir kt., 1994),
iteratyvioji lokalioji paieška (angl. iterated local search)
(Stützle, 2006), skruzdėlių kolonijų (Gambardella ir kt., 1999), bičių
spiečių (Dokeroglu ir kt., 2019) imitavimo algoritmai (angl. artificial
bee colony, ant colony optimization) ir kt. (Benlic, Hao, 2013;
Hafiz, Abdennour, 2016; Aksan ir kt., 2017; Abdel-Basset ir kt., 2018;
Chmiel, 2019). Nepaisant pasiektų daug žadančių rezultatų, euristinių
algoritmų KP uždaviniui tolesnio išvystymo ir tobulinimo klausimai vis dar
išlieka aktuali mokslinių tyrinėjimų tema.
eksponentine priklausomybe. Dėl šios priežasties KP uždavinio sprendimui
naudojami euristiniai optimizavimo algoritmai (Michalewicz, Fogel, 2000;
Yang, 2010; Edelkamp, Schrödl, 2012; Siarry, 2016). Nors šie algoritmai
negarantuoja optimalaus sprendinio suradimo, tačiau jie leidžia gauti
pakankamai aukštos kokybės (artimus optimaliems) sprendinius per priimtiną
skaičiavimų laiką. KP uždaviniui sėkmingai išbandyti šie euristiniai
algoritmai: atkaitinimo modeliavimas (angl. simulated annealing)
(Misevičius, 2003), genetiniai algoritmai (angl. genetic algorithms)
(Merz, Freisleben, 2000; Drezner, 2003; Misevicius, 2004; Tang ir kt., 2006;
Ahmed, 2015; Benlic, Hao, 2015; Chmiel, Kwiecień, 2018), tabu paieška (angl.
tabu search) (Taillard, 1991; Misevicius, 2005; Shylo, 2017),
godžiosios randomizuotos adaptyvios paieškos procedūros (angl. greedy
randomized adaptive search procedures (GRASP)) (Li ir kt., 1994),
iteratyvioji lokalioji paieška (angl. iterated local search)
(Stützle, 2006), skruzdėlių kolonijų (Gambardella ir kt., 1999), bičių
spiečių (Dokeroglu ir kt., 2019) imitavimo algoritmai (angl. artificial
bee colony, ant colony optimization) ir kt. (Benlic, Hao, 2013;
Hafiz, Abdennour, 2016; Aksan ir kt., 2017; Abdel-Basset ir kt., 2018;
Chmiel, 2019). Nepaisant pasiektų daug žadančių rezultatų, euristinių
algoritmų KP uždaviniui tolesnio išvystymo ir tobulinimo klausimai vis dar
išlieka aktuali mokslinių tyrinėjimų tema.
Šiame straipsnyje aprašomas patobulintas tabu paieškos (TP) algoritmas – vadinamasis dviejų lygių iteracinis tabu paieškos (ITP) algoritmas. Algoritmo veikimo principo naujoviškumas yra tas, kad tabu paieškos procedūra yra vykdoma iteraciniu būdu, pradedant vis nuo naujo sprendinio (pereinant tarp skirtingų lokaliai optimalių sprendinių). Iteracinį tabu paieškos algoritmą sudaro šie pagrindiniai komponentai: tabu paieškos procedūra, sprendinio-kandidato parinkimas, parinkto sprendinio mutavimas. TP procedūra atliekama kuo greičiau, panaudojant nedidelį iteracijų skaičių. Gautas TP procedūros sprendinys po to yra perturbuojamas mutavimo procedūroje tam, kad būtų diversifikuotas paieškos procesas, taip bandant išvengti paieškos stagnacijos, kas yra viena pagrindinių kliūčių vykdant standartinę, neiteracinę TP. Siekiant nustatyti galimą efektyviausią ITP modifikaciją, buvo tirta daugiau nei 10 mutavimo proceso realizavimo variantų.
Straipsnio struktūra yra tokia. Iš pradžių pateikiamos bazinės formuluotės. Po to aprašomas dviejų lygių iteracinis tabu paieškos algoritmas ir į jį integruotos sprendinių mutavimo procedūros. Taip pat pateikiami kompiuterinių-eksperimentinių tyrimų rezultatai, gauti išbandžius įvairius mutavimo procedūrų algoritminio realizavimo variantus. Straipsnis baigiamas apibendrinamosiomis pastabomis.
Dviejų lygių iteracinis tabu paieškos algoritmas
Bazinės formuluotės
Pradžioje pateikiame bazines formuluotes (apibrėžimus).
1. Tarkime, kad ![]() (
(![]() ) ir
) ir ![]() (
(![]() ,
, ![]() ) yra du
perstatymo (sprendinio)
) yra du
perstatymo (sprendinio) ![]() elementai, kurie vykdant
algoritmą gali būti sukeisti vietomis. Tuomet
elementai, kurie vykdant
algoritmą gali būti sukeisti vietomis. Tuomet ![]() apibrėšime taip:
apibrėšime taip:
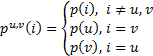 .
(2)
.
(2)
Tai reiškia, kad perstatymas ![]() gaunamas iš perstatymo
gaunamas iš perstatymo ![]() , tame
perstatyme sukeičiant elementus
, tame
perstatyme sukeičiant elementus ![]() ir
ir ![]() vietomis. Galima pastebėti,
kad galioja tokios lygybės:
vietomis. Galima pastebėti,
kad galioja tokios lygybės: ![]() ,
, ![]() ,
, ![]() . Taip pat bet kokiems
tarpusavyje skirtingiems
. Taip pat bet kokiems
tarpusavyje skirtingiems ![]() galioja
galioja ![]() ,
, ![]() .
.
2. Tikslo
funkcijos (![]() ) pokytis (
) pokytis (![]() ), sukeitus
sprendinio-perstatymo elementus
), sukeitus
sprendinio-perstatymo elementus ![]() ir
ir ![]() vietomis, apskaičiuojamas
pagal šią bendrą formulę:
vietomis, apskaičiuojamas
pagal šią bendrą formulę:
![]()
![]()
![]() .
(3)
.
(3)
Tikslo funkcijos pokytį dviem „perstatymams-kaimynams“ ![]() ir
ir ![]() , kai
, kai
![]() ,
galima apskaičiuoti ir žymiai greičiau – su sąlyga, jog yra įsimintos
(išsaugotos) visos ankstesnių pokyčių reikšmės
,
galima apskaičiuoti ir žymiai greičiau – su sąlyga, jog yra įsimintos
(išsaugotos) visos ankstesnių pokyčių reikšmės ![]() (
(![]() ). Pokyčiams saugoti pakanka
dvimatės matricos, o pokyčio reikšmė gaunama, panaudojant
). Pokyčiams saugoti pakanka
dvimatės matricos, o pokyčio reikšmė gaunama, panaudojant ![]() operacijų
(Taillard, 1991). Atlikus elementų
operacijų
(Taillard, 1991). Atlikus elementų ![]() ir
ir ![]() sukeitimą, naujos pokyčių
reikšmės
sukeitimą, naujos pokyčių
reikšmės ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ) apskaičiuojamos pagal šią formulę:
) apskaičiuojamos pagal šią formulę:
![]()
![]() +
+
![]() . (4)
. (4)
Pastaba. Jeigu
![]() arba
arba ![]() arba
arba ![]() arba
arba ![]() , tai turi būti
taikoma (3) formulė. Nors pastarosios formulės sudėtingumas yra
, tai turi būti
taikoma (3) formulė. Nors pastarosios formulės sudėtingumas yra ![]() , tačiau
ji taikoma tik keturioms indeksų poroms, o tai įgalina visas pokyčių
reikšmes apskaičiuoti panaudojant tik
, tačiau
ji taikoma tik keturioms indeksų poroms, o tai įgalina visas pokyčių
reikšmes apskaičiuoti panaudojant tik ![]() operacijų. Išimtį sudaro
inicializacijos fazė, t. y. pirmoji pokyčių apskaičiavimo iteracija, kurios
metu reikia (bet tik vieną kartą) atlikti
operacijų. Išimtį sudaro
inicializacijos fazė, t. y. pirmoji pokyčių apskaičiavimo iteracija, kurios
metu reikia (bet tik vieną kartą) atlikti ![]() operacijų.
operacijų.
Jeigu
matrica ![]() ir / arba matrica
ir / arba matrica ![]() yra simetrinė(s), tai (3)
formulė supaprastėja. Sakykime, kad matrica
yra simetrinė(s), tai (3)
formulė supaprastėja. Sakykime, kad matrica ![]() yra simetrinė. Tuomet galima
transformuoti (asimetrinę) matricą
yra simetrinė. Tuomet galima
transformuoti (asimetrinę) matricą ![]() į simetrinę matricą
į simetrinę matricą ![]() ; tam
pakanka sudėti atitinkamus matricos
; tam
pakanka sudėti atitinkamus matricos ![]() elementus. Taip gauname
žemiau pateikiamą formulę:
elementus. Taip gauname
žemiau pateikiamą formulę:
![]() ; (5)
; (5)
čia ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Analogiškai (4) formulė virsta tokia formule:
.
Analogiškai (4) formulė virsta tokia formule:
![]()
![]() . (6)
. (6)
Jeigu i = u(v) arba j = u(v), tai turi būti taikoma (5) formulė.
Disponuojant pakankamos apimties
kompiuterine atmintimi, galima vietoje dvimačių matricų ![]() ir
ir ![]() panaudoti
atitinkamas trimates matricas
panaudoti
atitinkamas trimates matricas ![]() ir
ir ![]() . Tarkime, kad
. Tarkime, kad
![]() ,
o
,
o ![]() , čia
, čia ![]() ,
, ![]() ,
, ![]() . Tuomet tikslo funkcijos
pokyčius galime apskaičiuoti panaudodami labai kompaktiškas
formules:
. Tuomet tikslo funkcijos
pokyčius galime apskaičiuoti panaudodami labai kompaktiškas
formules:
![]() , (7)
, (7)
![]() +
+![]() . (8)
. (8)
Matricoms ![]() ir
ir ![]() suformuoti panaudojama
suformuoti panaudojama ![]() operacijų; tas atliekama dar
prieš pradedant vykdyti algoritmą. Taigi, tai neturi kiek nors žymesnės
įtakos bendram algoritmo sudėtingumui; atvirkščiai, atlikti praktiniai
eksperimentai patvirtino išankstinę prielaidą, jog galima sutaupyti iki 20
proc. procesorinio laiko. (Aišku, kompiuterinės atminties sunaudojimas
išauga: matricų
operacijų; tas atliekama dar
prieš pradedant vykdyti algoritmą. Taigi, tai neturi kiek nors žymesnės
įtakos bendram algoritmo sudėtingumui; atvirkščiai, atlikti praktiniai
eksperimentai patvirtino išankstinę prielaidą, jog galima sutaupyti iki 20
proc. procesorinio laiko. (Aišku, kompiuterinės atminties sunaudojimas
išauga: matricų ![]() ,
, ![]() saugojimui reikia
saugojimui reikia ![]() atminties.)
atminties.)
3. Atstumas
(vadinamasis Hemingo atstumas) tarp dviejų perstatymų ![]() ir
ir ![]() apibrėžiamas kaip
apibrėžiamas kaip
![]() .
Galioja tokios lygybės:
.
Galioja tokios lygybės: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Pastebėsime, jog bet kuriems
. Pastebėsime, jog bet kuriems
![]() (
(![]() ,
,
![]() ,
,
![]() )
)
![]() .
Apskritai, jei turime
.
Apskritai, jei turime ![]() skirtingų
skirtingų ![]() , tai yra teisinga
ši lygybė:
, tai yra teisinga
ši lygybė: ![]() .
.
4. Sprendinio-perstatymo ![]() aplinka (porinių sukeitimų
aplinka)
aplinka (porinių sukeitimų
aplinka) ![]() apibrėžiama pagal formulę:
apibrėžiama pagal formulę: ![]() . Kitaip tariant, aplinką
. Kitaip tariant, aplinką
![]() sudaro sprendiniai:
sudaro sprendiniai: ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() , …,
, …, ![]() , …,
, …,
![]() ,
,
![]() ,
…,
,
…, ![]() , …,
, …, ![]() . Tokiu būdu aplinkos
. Tokiu būdu aplinkos ![]() dydis
dydis
![]() yra lygus
yra lygus ![]() . Tiek žingsnių reikia atlikti norint visiškai išnagrinėti
esamo sprendinio
. Tiek žingsnių reikia atlikti norint visiškai išnagrinėti
esamo sprendinio ![]() aplinką
aplinką ![]() . Taigi, šiai aplinkai
išnagrinėti pakanka
. Taigi, šiai aplinkai
išnagrinėti pakanka ![]() operacijų. Gali būti
apibrėžiamos ir kitokios aplinkos (bendruoju atveju sprendinio
operacijų. Gali būti
apibrėžiamos ir kitokios aplinkos (bendruoju atveju sprendinio ![]() aplinką
žymėsime
aplinką
žymėsime ![]() ). Sprendinių aplinkų visuma sudaro sprendinių paieškos aibę
(sprendinių paieškos erdvę).
). Sprendinių aplinkų visuma sudaro sprendinių paieškos aibę
(sprendinių paieškos erdvę).
5. Sprendinys ![]() vadinamas lokaliai optimaliu
sprendiniu aplinkos
vadinamas lokaliai optimaliu
sprendiniu aplinkos ![]() atžvilgiu, jeigu kiekvienam
sprendiniui
atžvilgiu, jeigu kiekvienam
sprendiniui ![]() iš aplinkos
iš aplinkos ![]() galioja
galioja ![]() (kitaip tariant,
sprendinio
(kitaip tariant,
sprendinio ![]() aplinkoje
aplinkoje ![]() nėra nė vieno geresnio
sprendinio už
nėra nė vieno geresnio
sprendinio už ![]() ).
).
6. Mutavimo (angl. mutation) procesas
sprendinių-perstatymų atveju gali būti apibrėžiamas panaudojant formalų
operatorių ![]() :
: ![]() . Taigi, jeigu
. Taigi, jeigu ![]() , tai
, tai ![]() ; be to,
; be to, ![]() . Galima
naudoti ir labiau formalizuotą operatorių
. Galima
naudoti ir labiau formalizuotą operatorių ![]() :
: ![]() , kuris esamą sprendinį
, kuris esamą sprendinį ![]() transformuoja į naują sprendinį
transformuoja į naują sprendinį ![]() ir tokį, jog
ir tokį, jog ![]() . Skaitytojas
galėtų įsitikinti, kad bet kuriam mutuotam sprendiniui-perstatymui
. Skaitytojas
galėtų įsitikinti, kad bet kuriam mutuotam sprendiniui-perstatymui ![]() egzistuoja skaičių seka
egzistuoja skaičių seka ![]() ir tokia, jog
ir tokia, jog ![]() . Dydį
(parametrą)
. Dydį
(parametrą) ![]() vadinsime mutavimo laipsniu (stiprumu). Akivaizdu, jog 2
vadinsime mutavimo laipsniu (stiprumu). Akivaizdu, jog 2![]() . Taigi,
po mutavimo pakinta
. Taigi,
po mutavimo pakinta ![]() procentų sprendinio elementų.
Parametras
procentų sprendinio elementų.
Parametras ![]() yra iš esmės vienintelis kiekybinis mutavimo procesą
reguliuojantis veiksnys. Kuo didesnė
yra iš esmės vienintelis kiekybinis mutavimo procesą
reguliuojantis veiksnys. Kuo didesnė ![]() reikšmė, tuo daugiau
sprendinio elementų sukeičiama (tuo didesniu mastu pakinta sprendinys, tuo
labiau mutuotas sprendinys „nutolsta“ nuo esamo sprendinio) ir atvirkščiai.
Galima šiuo atveju manyti, kad mutavimo operatorius
reikšmė, tuo daugiau
sprendinio elementų sukeičiama (tuo didesniu mastu pakinta sprendinys, tuo
labiau mutuotas sprendinys „nutolsta“ nuo esamo sprendinio) ir atvirkščiai.
Galima šiuo atveju manyti, kad mutavimo operatorius ![]() transformuoja
esamą sprendinį
transformuoja
esamą sprendinį ![]() į kitą sprendinį, priklausantį sprendinio
į kitą sprendinį, priklausantį sprendinio ![]() aplinkai
aplinkai ![]() . Dar
sakoma, jog atliekamas perėjimas (
. Dar
sakoma, jog atliekamas perėjimas (![]() perėjimas) iš sprendinio
perėjimas) iš sprendinio ![]() į
sprendinį
į
sprendinį ![]() (sprendinio
(sprendinio ![]() pakeitimas sprendiniu
pakeitimas sprendiniu ![]() ).
Atskiras mutavimo operatoriaus atvejis yra dviejų perstatymo elementų
sukeitimo operatorius
).
Atskiras mutavimo operatoriaus atvejis yra dviejų perstatymo elementų
sukeitimo operatorius ![]() :
: ![]() , kuris sukeičia perstatymo
u-tąjį ir v-tąjį elementus vietomis, t. y.
, kuris sukeičia perstatymo
u-tąjį ir v-tąjį elementus vietomis, t. y. ![]() . Daugelis
euristinių algoritmų KP uždaviniui remiasi būtent šio operatoriaus ir
aplinkos
. Daugelis
euristinių algoritmų KP uždaviniui remiasi būtent šio operatoriaus ir
aplinkos ![]() , kaip nereikalaujančios didelio skaičiavimų kiekio,
panaudojimu.
, kaip nereikalaujančios didelio skaičiavimų kiekio,
panaudojimu.
Grįždami prie mutavimo, pastebėsime, jog mutavimas kartu su kryžminimu yra pagrindiniai evoliucinių (genetinių) algoritmų operatoriai. Trumpai sakant, mutavimui savybingas grynai atsitiktinis pobūdis, mutavimo procesas savo prigimtimi yra indeterminuotas procesas. Tuo mutavimas iš esmės skiriasi nuo kryžminimo procedūrų. Mutavimo proceso metu generuojamos, apskritai kalbant, naujos sprendinių savybės, nauja informacija; o kryžminimo procedūros paprastai tik (re)kombinuoja informaciją, esančią pirmtakuose. Skirtingai negu standartinėse kryžminimo procedūrose, kur yra paveldimas sukauptas genetinis kodas iš dviejų pirmtakų ir daugiau niekur kitur, mutavimo procedūrose pagrindinis dalykas yra ne informacijos perdavimas, o kitos, naujos informacijos įnešimas, informacijos, kurios prieš tai dar nebuvo, sukūrimas. Šiuo požiūriu mutavimo procesas yra labiau kaip potencialaus naujumo generavimo procesas, kaip labiau kuriantysis, užuomazginis procesas, palyginti su kryžminimu. Be to, mutavimui nebūtina sprendinių populiacija, pakanka tik vieno sprendinio.
Tabu paieškos algoritmas
Skirtingai nuo tradicinių lokaliosios paieškos algoritmų, kurie apsiriboja vieno lokaliai optimalaus sprendinio suradimu, TP algoritmai tęsia paiešką ir tuo atveju, kai gauto sprendinio aplinkoje nebeegzistuoja geresnių sprendinių-kaimynų. Esminė TP idėja yra ta, jog yra (laikinai) uždraudžiama grįžti į tuos pačius, neseniai nagrinėtus sprendinius tam, kad būtų išvengta paieškos ciklinimosi, t. y. kartojimo nuo to paties išeities „taško“ (Glover, Laguna, 1997). Tam tikrais periodais atskiri sprendiniai yra uždraudžiami („įšaldomi“), skelbiami „tabu“. Laikinų draudimų strategija leidžia „neįstrigti“ lokaliųjų optimumų zonose ir suteikia galimybes po laikinų TF pablogėjimų tęsti paiešką naujose sprendinių erdvės srityse. Taip galima pereiti nuo vieno lokaliai optimalaus sprendinio prie kito, tikėtina, geresnio; tai kartojant daug kartų, žymiai išauga tikimybė surasti aukštesnės kokybės sprendinius.
Vykstant TP
procesui analizuojama esamojo sprendinio ![]() aplinka (mūsų atveju —
aplinka (mūsų atveju — ![]() ) ir
atliekamas tas nedraudžiamas perėjimas, kuris labiausiai pagerina (sumažina)
tikslo funkcijos
) ir
atliekamas tas nedraudžiamas perėjimas, kuris labiausiai pagerina (sumažina)
tikslo funkcijos ![]() reikšmę. Jeigu nėra pagerinančių perėjimų, tai pasirenkamas
tas, kuris mažiausiai pablogina TF reikšmę. Tam, kad būtų eliminuoti
paieškos ciklai, atvirkštinis perėjimas, taip pat grįžimas į kitus neseniai
aplankytus sprendinius turi būti uždraudžiamas apibrėžtam laikotarpiui.
Draudimai saugomi tabu atmintyje, t. y. sąraše
reikšmę. Jeigu nėra pagerinančių perėjimų, tai pasirenkamas
tas, kuris mažiausiai pablogina TF reikšmę. Tam, kad būtų eliminuoti
paieškos ciklai, atvirkštinis perėjimas, taip pat grįžimas į kitus neseniai
aplankytus sprendinius turi būti uždraudžiamas apibrėžtam laikotarpiui.
Draudimai saugomi tabu atmintyje, t. y. sąraše ![]() , įsimenant paskutinius
nagrinėtus sprendinius. Mūsų atveju tabu sąrašas
, įsimenant paskutinius
nagrinėtus sprendinius. Mūsų atveju tabu sąrašas ![]() realizuotas kaip dvimatė
realizuotas kaip dvimatė ![]() dydžio
matrica. Šiuo atveju matricos elementas
dydžio
matrica. Šiuo atveju matricos elementas ![]() saugo esamos iteracijos
numerį ir uždraudimo periodą (angl. tabu tenure)
saugo esamos iteracijos
numerį ir uždraudimo periodą (angl. tabu tenure) ![]() ; tokiu būdu ši
reikšmė nurodo, nuo kurios iteracijos vėl galima sukeisti perstatymo
i-tąjį ir j-tąjį narius. Parametro
; tokiu būdu ši
reikšmė nurodo, nuo kurios iteracijos vėl galima sukeisti perstatymo
i-tąjį ir j-tąjį narius. Parametro ![]() reikšmė mūsų ITP algoritme yra
prilyginta
reikšmė mūsų ITP algoritme yra
prilyginta ![]() . Elementų
. Elementų ![]() ,
, ![]() sukeitimas (perėjimas į
sprendinį
sukeitimas (perėjimas į
sprendinį ![]() ) yra negalimas, jeigu reikšmė
) yra negalimas, jeigu reikšmė ![]() yra didesnė negu esamas
paieškos iteracijos numeris. Draudimas yra anuliuojamas atsitiktiniais
momentais su labai maža tikimybe
yra didesnė negu esamas
paieškos iteracijos numeris. Draudimas yra anuliuojamas atsitiktiniais
momentais su labai maža tikimybe ![]() (
(![]() ). (Tai leidžia truputį
padidinti nedraudžiamų sprendinių kiekį ir ne taip apriboti galimas paieškos
kryptis.) Draudimas taip pat yra ignoruojamas, kai patenkinama aspiracijos
sąlyga (angl. aspiration criterion), t. y. po sukeitimo gaunamas
sprendinys, kuris yra geresnis už iki šiol atliekant tabu paieškos procedūrą
rastą geriausią sprendinį. Tabu sąrašas yra dinamiškai atnaujinamas vykdant
algoritmą (kai tik esamas sprendinys pakeičiamas nauju).
). (Tai leidžia truputį
padidinti nedraudžiamų sprendinių kiekį ir ne taip apriboti galimas paieškos
kryptis.) Draudimas taip pat yra ignoruojamas, kai patenkinama aspiracijos
sąlyga (angl. aspiration criterion), t. y. po sukeitimo gaunamas
sprendinys, kuris yra geresnis už iki šiol atliekant tabu paieškos procedūrą
rastą geriausią sprendinį. Tabu sąrašas yra dinamiškai atnaujinamas vykdant
algoritmą (kai tik esamas sprendinys pakeičiamas nauju).
Kartu su tabu
sąrašu mūsų tabu paieškos procedūra dar naudoja papildomą atmintį ![]() (antrinę
atmintį-archyvą (angl. secondary memory)) (Dell’amico, Trubian,
1998). Šios atminties paskirtis yra išsaugoti aukštos kokybės sprendinius,
kurie nors ir buvo įvertinti kaip labai geri, bet nebuvo pasirinkti.
Konkrečiai sakant, į antrinę atmintį kiekvienos iteracijos metu įtraukiami
sprendiniai, likę „antri“ po aplinkos
(antrinę
atmintį-archyvą (angl. secondary memory)) (Dell’amico, Trubian,
1998). Šios atminties paskirtis yra išsaugoti aukštos kokybės sprendinius,
kurie nors ir buvo įvertinti kaip labai geri, bet nebuvo pasirinkti.
Konkrečiai sakant, į antrinę atmintį kiekvienos iteracijos metu įtraukiami
sprendiniai, likę „antri“ po aplinkos ![]() patikrinimo. Jeigu vykdant
tabu paieškos procedūrą geriausias rastas sprendinys nesikeičia daugiau kaip
patikrinimo. Jeigu vykdant
tabu paieškos procedūrą geriausias rastas sprendinys nesikeičia daugiau kaip
![]() iteracijų, tai tabu sąrašas išvalomas ir paieška paleidžiama, pradedant nuo
vieno iš „antrųjų“ sprendinių iš antrinės atminties
iteracijų, tai tabu sąrašas išvalomas ir paieška paleidžiama, pradedant nuo
vieno iš „antrųjų“ sprendinių iš antrinės atminties ![]() (čia
(čia ![]() yra
nustatytas TP procedūros vykdymo iteracijų skaičius, o
yra
nustatytas TP procedūros vykdymo iteracijų skaičius, o ![]() – parinktas
tuščios eigos limito koeficientas, toks, jog
– parinktas
tuščios eigos limito koeficientas, toks, jog ![]() ). Reikia pastebėti, jog
archyve išsaugomos ir visos tikslo funkcijos pokyčių reikšmės (
). Reikia pastebėti, jog
archyve išsaugomos ir visos tikslo funkcijos pokyčių reikšmės (![]() ), tai
padidina atminties sąnaudas, bet skaičiavimų laikui tai labai didelės įtakos
nedaro. TP algoritmo sudėtingumas išlieka proporcingas
), tai
padidina atminties sąnaudas, bet skaičiavimų laikui tai labai didelės įtakos
nedaro. TP algoritmo sudėtingumas išlieka proporcingas ![]() , o tokio archyvo
panaudojimas, kaip rodo eksperimentų rezultatai, prisideda prie to, jog
efektyvumas padidėja dėl to, jog sumažinamas neigiamas paieškos stagnacijos
poveikis. Antrinė atmintis išvaloma, pasibaigus TP procedūrai.
, o tokio archyvo
panaudojimas, kaip rodo eksperimentų rezultatai, prisideda prie to, jog
efektyvumas padidėja dėl to, jog sumažinamas neigiamas paieškos stagnacijos
poveikis. Antrinė atmintis išvaloma, pasibaigus TP procedūrai.
TP
procesas yra baigiamas, kai tik atliekamas iš anksto pasirinktas TP vykdymo
iteracijų skaičius (![]() ). TP algoritmo detalizuotas
formalus aprašymas pateiktas 1 pav.
). TP algoritmo detalizuotas
formalus aprašymas pateiktas 1 pav.
procedure Tabu_Paieška; // tabu paieškos algoritmas KP uždaviniui
// duomenys: p - esamas sprendinys-perstatymas (kartu su atitinkamais tikslo funkcijos reikšmių pokyčiais (Δ)),
// n - uždavinio dydis (perstatymo dydis)
// rezultatai: p• - geriausias rastas sprendinys (kartu su TF reikšmių pokyčiais)
// valdymo parametrai: τ - tabu paieškos vykdymo iteracijų skaičius, h - uždraudimo (tabu) periodas,
// α - tabu paieškos randomizavimo koeficientas, β - tuščios eigos limito koeficientas
begin
p• := p; k := 1; k′ := 1; archyvo_skaitiklis := 0; L := ![]() ; // L - tuščios eigos
limitas
; // L - tuščios eigos
limitas
while (k ≤ τ) begin // pagrindinis tabu paieškos iteracijų vykdymo ciklas
delta′min := ∞; delta′′min := ∞; u′ := 1; v′ := 2;
// nagrinėjama sprendinio p aplinka Θ2(p) ir ieškomas geriausias sprendinys, kuris nėra uždraustas (tabu)
for i := 1 to n - 1 do
for j := i + 1 to n do begin
delta := Δ (pi, j, p);
tabu := iif((tij ≥ k) and (random() ≥ α), TRUE, FALSE); aspiracija := iif(z(p) + delta < z(p•), TRUE, FALSE);
if ((delta < delta′min) and (tabu = FALSE)) or (aspiracija = TRUE) then begin
if delta < delta′min then begin
delta′′min := delta′min; u′′ := u′; v′′ := v′; delta′min := delta; u′ := i; v′ := j endif
else if delta < delta′′min then begin delta′′min := delta; u′′ := i; v′′ := j endif
endif
endfor;
if delta′′min < ∞ then begin // „antrojo“ sprendinio įtraukimas į archyvą (antrinę atmintį) G
archyvo_skaitiklis := archyvo_skaitiklis + 1; Γ [archyvo_skaitiklis] ← p, Δ, u′′, v′′ endif;
if delta′min < ∞ then begin
![]() ; // esamas sprendinys
pakeičiamas nauju sprendiniu
; // esamas sprendinys
pakeičiamas nauju sprendiniu
perskaičiuoti tikslo funkcijos pokyčius
![]() , i, j = 1, ..., n;
, i, j = 1, ..., n;
if z(p) < z(p•) then begin p• := p; k′ := k endif; // išsaugomas geriausias rastas sprendinys
![]() // elementų
p(u′), p(v′)
sukeitimas uždraudžiamas būsimoms h iteracijų
// elementų
p(u′), p(v′)
sukeitimas uždraudžiamas būsimoms h iteracijų
endif;
if (k - k′ > L) and (k <τ - L) then begin // tabu paieškos paleidimas, panaudojant sprendinį iš archyvo
išvalyti tabu sąrašą T;
atsitiktinio_išrinkimo_indeksas := random(archyvo_skaitiklis * 0.8, archyvo_skaitiklis);
p, Δ, u′′, v′′ ← Γ[atsitiktinio_išrinkimo_indeksas];
![]() :=
:= ![]() ; perskaičiuoti tikslo funkcijos pokyčius
; perskaičiuoti tikslo funkcijos pokyčius
![]() , i, j = 1, ..., n;
, i, j = 1, ..., n;
![]() ; k′ := k
; k′ := k
endif;
k := k + 1
endwhile;
išvalyti tabu sąrašą T
end.
Pastabos. 1. Tiesioginio vykdymo „if“ funkcija iif(x, y1, y2) grąžina y1, jeigu x = TRUE, kitu atveju grąžinama y2. 2. Funkcija random() generuoja (pseudo)atsitiktinį realųjį skaičių, patenkantį į intervalą [0, 1]. 3. Funkcija random(x1, x2) generuoja (pseudo)atsitiktinį sveikąjį skaičių iš intervalo [x1, x2].
1 pav. Tabu paieškos algoritmo aprašymas
Iteracinis tabu paieškos algoritmas
Tabu paieškos algoritmo panaudojimas dar neužtikrina aukštos surastų sprendinių kokybės dėl jau minėto paieškos stagnacijos efekto pasireiškimo. Vienas iš būdų sumažinti paieškos stagnavimo poveikį yra išplėsti standartinį TP algoritmą taip, kad jis būtų vykdomas ne vieną, bet keletą kartų. Taip gaunama iteratyvioji tabu paieška (ITP) (angl. iterated tabu search), kurios veikimo principo pagrindas yra daugkartinis TP algoritmo panaudojimas, iteratyviu būdu vykdant TP kartotinį procesą ir kombinuojant tabu paiešką su papildomomis sprendinių pertvarkymo, t. y. mutavimo, procedūromis[2]. Iteratyviajai tabu paieškai, savo ruožtu, taip pat gali būti taikomas daugkartinis panaudojimas; taip gaunamas 2 lygių iteratyviosios tabu paieškos algoritmas – savotiškas hierarchinis iteratyviosios tabu paieškos algoritmas. Tokio tipo algoritmo skiriamoji savybė yra ta, jog jis pasižymi savo struktūros hierarchiškumu, tiksliau, panašumumu į save (angl. self-similarity). Panašumas į save, kaip žinoma, yra turbūt vienas iš fundamentaliausių gamtos principų. Mūsų atveju dviejų lygių ITP algoritmą sudaro du panašūs į save struktūriniai lygiai. Aukštesniojo (2-ojo) lygmens algoritmas kreipiasi į žemesniojo (1-ojo) lygio algoritmą, kuris jau betarpiškai naudoja TP algoritmą. Šiuo atveju TP procedūra, galima įsivaizduoti, yra savotiškas iteracinio algoritmo „branduolys“. Būtent ši ir tik ši procedūra vykdo betarpišką sprendinio pagerinimą (atlieka paieškos intensifikavimą).
Du lygiai yra iš esmės tos pačios struktūros. Esamo lygio algoritmą sudaro trys esminiai komponentai: 1) žemesnio lygio algoritmo panaudojimas (iškvietimas); 2) sprendinio-kandidato parinkimas mutavimui; 3) atrinkto sprendinio mutavimas. Nors atskirų lygių struktūra yra išties paprasta, tačiau šių lygių tinkamas sujungimas leidžia žymiai padidinti paieškos efektyvumą. Aišku, paieškos laikas išauga, bet tai yra kompensuojama aukštesne rezultatų kokybe. Atkreiptinas dėmesys į tai, kad sprendinio mutavimas yra labai svarbus komponentas ITP algoritme ir jis yra reikalingas tam, kad būtų galima pereiti į kitas, nenagrinėtas sprendinių aibės (paieškos erdvės) sritis ir išvengti paieškos stagnacijos. Matyti, jog sprendinio mutavimas vykdomas kiekviename lygyje – skirtingai nuo „branduolio“ procedūros (TP procedūros), kuri atliekama tik žemiausiame lygyje. Taigi, iteracinio algoritmo atveju dominuoja paieškos diversifikavimo faktorius, o tai ir yra labai svarbu, vykdant paiešką didžiulėje sprendinių erdvėje su daug lokaliai optimalių sprendinių. Kas dėl sprendinio-kandidato parinkimo mutavimui, tai visada imamas paskutinis gautas (vis kitas) pagerintas sprendinys. Toks parinkimas leidžia išžvalgyti galimai didesnę sprendinių erdvės dalį.
Vieno ir dviejų lygių ITP algoritmų detalizuoti formalūs aprašymai pateikti 2 ir 3 pav.
procedure 1-Lygio_Iteracinė_Tabu_Paieška; // vieno lygio iteracinės tabu paieškos algoritmas KP uždaviniui
// duomenys: p - esamas sprendinys-perstatymas
// rezultatai: pÑ - geriausias rastas sprendinys-perstatymas (kartu su tikslo funkcijos reikšmių pokyčiais (Δ))
// valdymo parametras: Q1 - 1 lygio tabu paieškos vykdymo iteracijų skaičius
begin
pÑ := p;
for q1 := 1 to Q1 do begin
vykdyti procedūrą Tabu_Paieška sprendiniui p, gauti (pagerintą) sprendinį p•;
if z(p•) < z(pÑ) pÑ := p•; // įsimenamas geriausias rastas sprendinys (kartu su TF pokyčiais)
if q1 < Q1 then begin
p := Sprendinio_Kandidato_Parinkimas_Mutavimui(p·, pÑ);
vykdyti mutavimo procedūrą sprendiniui p, grąžinti mutuotą sprendinį p~;
p := p~
endif
endfor
end.
2 pav. Vieno lygio iteracinės tabu paieškos algoritmo aprašymas
procedure 2-jų_Lygių_Iteracinė_Tabu_Paieška; // dviejų lygių iteracinės tabu paieškos algoritmas KP uždaviniui
// duomenys: p° - pradinis sprendinys-perstatymas
// rezultatai: pÑÑ - geriausias rastas sprendinys-perstatymas
// valdymo parametras: Q2 - 2 lygio tabu paieškos vykdymo iteracijų skaičius
begin
generuoti atsitiktiniu būdu pradinį sprendinį-perstatymą p°;
apskaičiuoti tikslo funkcijos pokyčius
![]() , i, j = 1, ..., n;
, i, j = 1, ..., n;
inicializuoti tabu sąrašą T;
p := p°; pÑÑ := p°;
for q2 := 1 to Q2 do begin
vykdyti procedūrą 1-Lygio_Iteracinė_Tabu_Paieška sprendiniui p, gauti (pagerintą) sprendinį pÑ;
if z(pÑ) < z(pÑÑ) pÑÑ := pÑ; // įsimenamas geriausias rastas sprendinys
if q2 < Q2 then begin
p := Sprendinio_Kandidato_Parinkimas_Mutavimui(pÑ, pÑÑ);
vykdyti mutavimo procedūrą sprendiniui p, grąžinti mutuotą sprendinį p~;
p := p~
endif
endfor
end.
3 pav. Dviejų lygių iteracinės tabu paieškos algoritmo aprašymas
Mutavimo proceso
bazinių variantų algoritminis realizavimas nėra labai sudėtingas. Teorinis
pagrindas yra mutavimo operatorius ![]() , formaliai aprašytas sk.
„Bazinės formuluotės“. Atsižvelgiant į mutavimo algoritminio realizavimo
skirtumus (ypatumus), galima sudaryti įvairių tipų mutavimo
procedūras.
, formaliai aprašytas sk.
„Bazinės formuluotės“. Atsižvelgiant į mutavimo algoritminio realizavimo
skirtumus (ypatumus), galima sudaryti įvairių tipų mutavimo
procedūras.
Toliau trumpai aprašomos mūsų sudarytos ir tyrime naudotos mutavimo procedūros.
Atsitiktiniai poriniai elementų sukeitimai
Ši mutavimo procedūra yra labai nesudėtinga (žr.
4 pav.). Sukuriamas sprendinio-perstatymo ![]() klonas
klonas ![]() . Perstatyme
. Perstatyme ![]() atsitiktinai parenkamos pozicijos
atsitiktinai parenkamos pozicijos ![]() ,
, ![]() , sugeneruojant du skirtingus
(pseudo)atsitiktinius sveikuosius skaičius iš intervalo
, sugeneruojant du skirtingus
(pseudo)atsitiktinius sveikuosius skaičius iš intervalo ![]() pagal tolygiojo
pasiskirstymo dėsnį. (Kad būtų išvengta pasikartojančių atsitiktinių skaičių
generavimo, yra iš anksto sugeneruojamas perstatymas
pagal tolygiojo
pasiskirstymo dėsnį. (Kad būtų išvengta pasikartojančių atsitiktinių skaičių
generavimo, yra iš anksto sugeneruojamas perstatymas ![]() , sudarytas iš
atsitiktinai sumaišytų sveikųjų skaičių nuo
, sudarytas iš
atsitiktinai sumaišytų sveikųjų skaičių nuo ![]() iki
iki ![]() . Skaičių poros
. Skaičių poros ![]() tokiu būdu nurodo
perstatymo
tokiu būdu nurodo
perstatymo ![]() atsitiktinių pozicijų indeksų poras.) Pradedama nuo poros
atsitiktinių pozicijų indeksų poras.) Pradedama nuo poros ![]() , ir
perstatymo
, ir
perstatymo ![]() elementai, esantys šiose pozicijose, sukeičiami (iš
elementai, esantys šiose pozicijose, sukeičiami (iš ![]() pereinama į
pereinama į ![]() ). Po to imama pora
). Po to imama pora ![]() ir t. t. Tai kartojama
ir t. t. Tai kartojama ![]() skaičių
kartų; čia
skaičių
kartų; čia ![]() – algoritmo tyrėjo / vartotojo iš anksto nustatyta (norima)
mutavimo laipsnio reikšmė. Mutavimo procedūros rezultatas – mutuotas
sprendinys
– algoritmo tyrėjo / vartotojo iš anksto nustatyta (norima)
mutavimo laipsnio reikšmė. Mutavimo procedūros rezultatas – mutuotas
sprendinys ![]() , tenkinantis sąlygą
, tenkinantis sąlygą ![]() . Aišku, kad formuojant
mutuotą sprendinį-perstatymą yra užtikrinamas reikalavimas, jog gautame
sprendinyje-perstatyme jokie elementai nesikartoja, t. y.,
. Aišku, kad formuojant
mutuotą sprendinį-perstatymą yra užtikrinamas reikalavimas, jog gautame
sprendinyje-perstatyme jokie elementai nesikartoja, t. y., ![]() . Mutavimo proceso
stiprumas kontroliuojamas panaudojant parametrą
. Mutavimo proceso
stiprumas kontroliuojamas panaudojant parametrą ![]() (teoriškai 2
(teoriškai 2![]() ).
).
Remiantis šiuo mutavimo algoritmo principu galima sudaryti ir daug įvairių kitų modifikuotų mutavimo procedūrų.
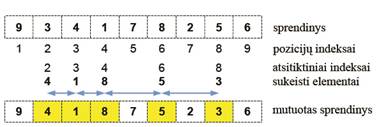
4 pav. Mutavimo
procedūros pavyzdžio iliustracija (n = 9, m = 5)
(Šiame pavyzdyje
mutavimo procesas yra toks: elementas 3 keičiamas su elementu 4 (elementas 3
patenka į 3-iąją poziciją); 3 (esantis 3-iojoje pozicijoje) keičiamas su 1;
3 (esantis 4-ojoje pozicijoje) keičiamas su 8; 3 (esantis 6-ojoje
pozicijoje) keičiamas su 5 (3 patenka į 8-ąją
poziciją))
Poriniai elementų sukeitimai panaudojant atsitiktinį raktą
Mutavimo procedūrą šiuo atveju sudaro
du žingsniai: 1) atsitiktiniai poriniai elementų sukeitimai; 2) sukeistų
elementų išmaišymas, panaudojant atsitiktinį raktą. Atsitiktinis raktas yra
papildomas atsitiktinių indeksų nuo ![]() iki
iki ![]() masyvas (rinkinys
masyvas (rinkinys ![]() ).
Atsitiktinio rakto reikšmės nurodo, kokie anksčiau sukeisti elementai su
kokiais elementais maišomi. Taip bandoma gauti „giliau“ mutuotą sprendinį,
daugiau randomizuotą elementų išmaišymą. Tuomet vykstant TP procesui ne taip
paprasta grįžti į ankstesnę situaciją, tik atliekant porinius elementų
sukeitimus.
).
Atsitiktinio rakto reikšmės nurodo, kokie anksčiau sukeisti elementai su
kokiais elementais maišomi. Taip bandoma gauti „giliau“ mutuotą sprendinį,
daugiau randomizuotą elementų išmaišymą. Tuomet vykstant TP procesui ne taip
paprasta grįžti į ankstesnę situaciją, tik atliekant porinius elementų
sukeitimus.
Mutavimas panaudojant priešines (opozicines) reikšmes
Šioje mutavimo procedūroje sprendinio ![]() klone
klone
![]() atsitiktinai parenkama pozicija, tarkime,
atsitiktinai parenkama pozicija, tarkime, ![]() . Tuomet sprendinio
. Tuomet sprendinio ![]() esama
elemento reikšmė
esama
elemento reikšmė ![]() pakeičiama tokia priešine (opozicine) (angl.
opposition) reikšme:
pakeičiama tokia priešine (opozicine) (angl.
opposition) reikšme: ![]() , čia
, čia ![]() žymi liekanos
gavimo operaciją. Po šio sukeitimo taip pat turi būti pakeistas sprendinio
elementas, kuris prieš tai buvo lygus
žymi liekanos
gavimo operaciją. Po šio sukeitimo taip pat turi būti pakeistas sprendinio
elementas, kuris prieš tai buvo lygus ![]() . Po abiejų sukeitimų
. Po abiejų sukeitimų ![]() tampa
lygus
tampa
lygus ![]() ,
, ![]() – lygus
– lygus ![]() ,
, ![]() rodo sprendinio
rodo sprendinio ![]() elemento
reikšmės, kuri buvo lygi
elemento
reikšmės, kuri buvo lygi ![]() ,
indeksą.
,
indeksą.
Maksimalaus elementų atstumo mutavimas
Duotoje procedūroje sukeičiamų sprendinio elementų pozicijų
indeksai generuojami taip, jog atstumas (![]() ) tarp tų pozicijų būtų galimai
didesnis. Panaudota tokia sukeičiamų sprendinio elementų indeksų reikšmių
) tarp tų pozicijų būtų galimai
didesnis. Panaudota tokia sukeičiamų sprendinio elementų indeksų reikšmių
![]() generavimo formulė:
generavimo formulė: ![]() , čia
, čia ![]() ,
, ![]() –
(pseudo)atsitiktinis realusis skaičius iš intervalo
–
(pseudo)atsitiktinis realusis skaičius iš intervalo ![]() ,
, ![]() ,
, ![]() ; pradinė
; pradinė ![]() reikšmė
(
reikšmė
(![]() )
– tai atsitiktinis sveikasis skaičius iš intervalo
)
– tai atsitiktinis sveikasis skaičius iš intervalo ![]() . Tokiu būdu yra
sugeneruojama
. Tokiu būdu yra
sugeneruojama ![]() atsitiktinių indeksų reikšmių (priminsime, kad
atsitiktinių indeksų reikšmių (priminsime, kad ![]() yra mutavimo
laipsnis). Šiuo atveju rekomenduojama, kad
yra mutavimo
laipsnis). Šiuo atveju rekomenduojama, kad ![]() neviršytų
neviršytų ![]() .
.
Modifikuotas atsitiktinių elementų sukeitimų mutavimas - I
Ši procedūra panaši į
atsitiktinių porinių elementų sukeitimų mutavimo procedūrą. Generuojamas
atsitiktinių realiųjų skaičių iš intervalo ![]() rinkinys (angl. real-coded
values). Sugeneruoti skaičiai (kartu su juos atitinkančiais teigiamais
indeksais (angl. smallest positive values)) išrikiuojami didėjimo
tvarka. Išrikiuotus atsitiktinius skaičius atitinkantys išmaišyti indeksai
ir nurodo, kurias sprendinio
rinkinys (angl. real-coded
values). Sugeneruoti skaičiai (kartu su juos atitinkančiais teigiamais
indeksais (angl. smallest positive values)) išrikiuojami didėjimo
tvarka. Išrikiuotus atsitiktinius skaičius atitinkantys išmaišyti indeksai
ir nurodo, kurias sprendinio ![]() elementų poras reikia sukeisti
(žr. sk. „Atsitiktiniai poriniai elementų
sukeitimai“).
elementų poras reikia sukeisti
(žr. sk. „Atsitiktiniai poriniai elementų
sukeitimai“).
Modifikuotas atsitiktinių elementų sukeitimų mutavimas - II
Duota procedūra yra irgi panaši
į procedūrą, aprašytą sk. „Atsitiktiniai poriniai elementų sukeitimai“.
Procedūros tikslas – nuosekliai, vienas po kito generuojant atsitiktinius
sveikuosius skaičius iš intervalo ![]() , iš karto gauti sprendinio
, iš karto gauti sprendinio
![]() sukeičiamų elementų porų indeksus. Tačiau, kaip pastebėta, atsitiktiniai
sveikieji skaičiai gali dubliuotis. Tam, kad nebūtų dubliavimosi,
sugeneruoti atsitiktiniai sveikieji skaičiai surikiuojami (žr. sk.
„Modifikuotas atsitiktinių elementų sukeitimų mutavimas - I“). Surikiuotus
skaičius atitinkantys indeksai nurodo reikalingus sumaišyti
elementus.
sukeičiamų elementų porų indeksus. Tačiau, kaip pastebėta, atsitiktiniai
sveikieji skaičiai gali dubliuotis. Tam, kad nebūtų dubliavimosi,
sugeneruoti atsitiktiniai sveikieji skaičiai surikiuojami (žr. sk.
„Modifikuotas atsitiktinių elementų sukeitimų mutavimas - I“). Surikiuotus
skaičius atitinkantys indeksai nurodo reikalingus sumaišyti
elementus.
Kombinuoto mutavimo procedūra
Kombinuoto mutavimo procedūroje yra nuosekliai sujungtos dvi mutavimo procedūros. Iš pradžių nustatomi atsitiktiniai perstatymo elementų indeksai, kaip aprašyta sk. „Modifikuotas atsitiktinių elementų sukeitimų mutavimas - II“. Po to nustatyti elementai yra mutuojami, panaudojant priešines reikšmes (žr. sk. „Mutavimas panaudojant priešines (opozicines) reikšmes“).
Randomizuotos lokalios paieškos mutavimas
Šiuo atveju iš pradžių vykdomi atsitiktiniai poriniai elementų sukeitimai (kaip aprašyta sk. „Atsitiktiniai poriniai elementų sukeitimai“). Po to atliekama randomizuota lokalioji paieška, t. y. nuosekliai nagrinėjamos atsitiktinai parinktos sprendinio elementų poros, bet elementų sukeitimai atliekami tik tuo atveju, jeigu po sukeitimo gaunamas geresnis sprendinys (tikslo funkcijos reikšmė sumažėja). Ši ir kitos toliau aprašomos mutavimo procedūros jau nėra tokios universalios (nepriklausančios nuo sprendžiamo uždavinio), kaip anksčiau aprašytos, nes turi būti įvertinama ir tikslo funkcija bei specifinės konkretaus sprendžiamo uždavinio savybės.
Randomizuotos dalinės lokalios paieškos mutavimas
Šioje procedūroje iš pradžių taip pat vykdomi atsitiktiniai elementų sukeitimai. Po to atliekama dalinė randomizuota lokalioji paieška. Šiuo atveju visiškai išnagrinėjama atsitiktiniu būdu sukonstruota, nedidelės apimties sprendinių aplinka. Vykdant paiešką šioje aplinkoje, vėlgi atliekami tik tie perėjimai tarp sprendinių, kurie pagerina tikslo funkcijos reikšmę.
Godžios adaptyvios paieškos mutavimas
Šios mutavimo procedūros principas yra kiek kitoks negu
prieš tai nagrinėtų. Ypatumas yra tas, jog iš pradžių sprendinys savotiškai
„dezintegruojamas“, po to rekonstruojamas. Sprendinio dezintegravimas
reiškia, jog yra anuliuojama (pašalinama) dalis atsitiktinai parinktų
sprendinio elementų, sprendinys tampa dalinis, po to bandoma dalinį
sprendinį rekonstruoti į pilnąjį sprendinį ir taip, kad gautas sprendinys
būtų su kuo mažesne tikslo funkcijos reikšme. Taigi, mutavimą sudaro dvi
fazės: 1) sprendinio dezintegravimas, kuris yra atsitiktinis; 2) sprendinio
rekonstravimas, kuris yra determinuotas (nes siekiama minimizuoti tikslo
funkciją). Mūsų procedūroje pirmos fazės metu yra anuliuojama ![]() elementų, t. y.
tiek, koks yra mutavimo laipsnis. Antroje fazėje taikomas godusis
konstravimo algoritmas. Šis algoritmas iš visų galimų
elementų, t. y.
tiek, koks yra mutavimo laipsnis. Antroje fazėje taikomas godusis
konstravimo algoritmas. Šis algoritmas iš visų galimų ![]() variantų atrenka
tą, kuriam apskaičiuotas tikslo funkcijos įvertinimas (tam tikra tikslo
funkcijos ribos reikšmė) yra minimalus. Mutavimo laipsnio
variantų atrenka
tą, kuriam apskaičiuotas tikslo funkcijos įvertinimas (tam tikra tikslo
funkcijos ribos reikšmė) yra minimalus. Mutavimo laipsnio ![]() dydis yra
apribotas (
dydis yra
apribotas (![]() ,
, ![]() ), kad labai neišaugtų mutavimo procedūros atlikimo
laikas.
), kad labai neišaugtų mutavimo procedūros atlikimo
laikas.
Godžios randomizuotos adaptyvios paieškos mutavimas
Ši mutavimo procedūra primena prieš tai aprašytąją. Skirtumas yra tas, jog dalinio sprendinio rekonstravimo fazėje yra naudojamas godžios randomizuotos adaptyvios paieškos algoritmas (angl. greedy randomized adaptive search procedure – GRASP) (Li ir kt., 1994), norint gauti pagerintą sprendinį.
Išsklaidytas (išsklaidytos tabu paieškos) mutavimas
Šiuo atveju atliekant mutavimo procedūrą yra
tiesiog pertvarkytas tabu paieškos algoritmas, kuriame atliekami tik
perėjimai tarp „antrųjų“ sprendinių. Atliekamas ribotas TP vykdymo iteracijų
skaičius (![]() iteracijų). Taigi, mutavimas tampa ne tiek atsitiktinis, kiek
godus (kvazideterminuotas).
iteracijų). Taigi, mutavimas tampa ne tiek atsitiktinis, kiek
godus (kvazideterminuotas).
Pastebėtina, kad, atliekant visas mutavimo
procedūras, pasikeičia sprendinio TF reikšmė, taigi yra labai svarbu
efektyviai perskaičiuoti TF reikšmių pokyčius. Kaip žinoma, TF pokyčiai,
sukeitus du elementus, apskaičiuojami panaudojant ![]() operacijų. Kadangi visos
aprašytos mutavimo procedūros atlieka apytikriai
operacijų. Kadangi visos
aprašytos mutavimo procedūros atlieka apytikriai ![]() ar panašų (proporcingą)
skaičių elementų sukeitimų, tai visų mūsų mutavimo procedūrų sudėtingumas
yra proporcingas
ar panašų (proporcingą)
skaičių elementų sukeitimų, tai visų mūsų mutavimo procedūrų sudėtingumas
yra proporcingas ![]() .
.
Mutavimo laipsnis ![]() atlieka svarbų vaidmenį
mutavimo procedūroje, o kartu ir ją naudojančiame iteraciniame tabu paieškos
algoritme. Turi būti pasirenkamas tam tikras kompromisinis variantas tarp
dviejų ekstremalių situacijų: 1) reikšmė
atlieka svarbų vaidmenį
mutavimo procedūroje, o kartu ir ją naudojančiame iteraciniame tabu paieškos
algoritme. Turi būti pasirenkamas tam tikras kompromisinis variantas tarp
dviejų ekstremalių situacijų: 1) reikšmė ![]() yra (labai) maža; 2) reikšmė
yra (labai) maža; 2) reikšmė
![]() yra
(labai) didelė (pvz., artima
yra
(labai) didelė (pvz., artima ![]() ). Pirmuoju atveju mutavimas
negarantuotų pakankamai „nutolusio“ (nuo duotojo) sprendinio generavimo, o
tai lemtų grįžimą atgal į ankstesnįjį lokalųjį optimumą po tabu paieškos
etapo. Antruoju atveju paieška taptų labai panaši į daugkartinę paiešką,
startuojant kiekvieną kartą tiesiog nuo atsitiktinių sprendinių ir
prarandant paieškos metu lokaliai optimaliuose sprendiniuose sukauptą
naudingą informaciją.
). Pirmuoju atveju mutavimas
negarantuotų pakankamai „nutolusio“ (nuo duotojo) sprendinio generavimo, o
tai lemtų grįžimą atgal į ankstesnįjį lokalųjį optimumą po tabu paieškos
etapo. Antruoju atveju paieška taptų labai panaši į daugkartinę paiešką,
startuojant kiekvieną kartą tiesiog nuo atsitiktinių sprendinių ir
prarandant paieškos metu lokaliai optimaliuose sprendiniuose sukauptą
naudingą informaciją.