Ekonomika ISSN 1392-1258 eISSN 2424-6166
2019, vol. 98(2), pp. 55–75 DOI: https://doi.org/10.15388/Ekon.2019.2.4
The Impact of Excise Tax Increases on Ethyl Alcohol Sales in Lithuania
Algirdas Bartkus*
Vilnius University, Lithuania
Abstract. This article provides empirical evidence that the demand for ethyl alcohol in Lithuania is price elastic and the root cause of this elasticity is the competition between Lithuanian and Polish sellers. The basis for the emergence of competition lies in the price differences between the countries, which arise as a direct consequence of the Lithuanian government’s policy in the alcohol sector, which is directed towards reckless increases in excise duties. The increase in Lithuanian excise duties leads to a wider price gap between countries and in the first months after the increase results increases in prices. In subsequent months, Lithuanian importers and manufacturers tend to revise the assortment and costs, replacing more expensive goods with cheaper ones or slightly alter the markups. These changes are the main reason why demand in the domestic market gradually recovers. The price elasticity of demand predetermines the gradual recovery of the ethyl alcohol market, but each increase in excise duty reduces the manufacturers’ markups and (or) leads to the changes in product range, where higher-costs products are displaced by lower-cost products.
Keywords: alcohol market, public sector economics, non-linear econometric models.
* Corresponding author:
Department of Quantitative Methods and Modelling, Faculty of Economics and Business Administration, Vilnius University, 9 Saulėtekio Ave., Building II, LT-10222, Vilnius, Lithuania.
Email: algirdas.bartkus@evaf.vu.lt
Received: 21/10/2019. Revised: 22/11/2019. Accepted: 01/12/2019
Copyright © 2019 Algirdas Bartkus. Published by Vilnius University Press
This is an Open Access article distributed under the terms of the Creative Commons Attribution Licence, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
1. Introduction
Taxes affect prices, but the majority of taxes have an indirect effect on prices. Despite being indirect, these effects sometimes can be easily traced out, e.g., whether the increase in corporate taxes is in any direct way related to pricing policies, but this increase may lead to the revision of markup. The possible effect on the prices can be easily foreseen because corporate taxes have the effect on the net income of price setters. This does not imply that prices won’t change if certain taxes, which do not affect the prices or the level of income of the prices setters directly, are changed. Let us consider the effect of increases in income tax. This increase may not affect the prices at all if the level of unemployment is high and the bargaining power of the workers is weak – it will only lower the purchasing power of the consumers. But if the income taxes are raised during the economic expansion period, this may as well lead to the increases in prices. If the level of unemployment is low, the workers dominate the wage bargaining process, and the government’s plans to raise the income taxes will result in the extra increases in the nominal wages in order to offset the purchasing losses that will occur from tax increments. In other words, the plans to increase the income taxes will result in faster wage hikes. If that happens, firms will face a significant increase in labour costs that won’t be offset by the increases in demand, and in order to keep the profits or profitability at the same level, the final price of a product will go up as well.
In this article we are dealing with a very simple tax – excise tax on alcohol and in particular on ethyl alcohol. Ethyl alcohol is one of the three major alcohol products, while others are wine and beer. This group of beverages deserves special attention because it is chosen by both frequent and occasional drinkers, especially those who are older when it comes to the last group (Karpuškienė et al., 2019). Excise taxes have to be treated differently from corporate or income taxes, as it is frequently assumed that these taxes are usually borne by consumers. No doubt that this is true for the initial months, after the increase took place, but no one should be assured that this will stay so also in the later months following the increase. Corporate taxes, although placed on businesses, can be transferred onto the consumers via the hikes in the markup. Income taxes may be transferred onto the consumers via the hikes in costs. Excise taxes are placed on the consumers directly, and if all other things stay the same, the increase in excise tax has to increase the final price proportionally. The question of main interest here is how long this change will last and what are the conditions that are responsible for all the possible changes in prices.
The initial impression of how excise taxes affect the final price may be summarised in the following equation:
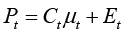 (1)
(1)
Here Pt is the final price, that is the sum of costs Ct, that are augmented by the markup μt and excise tax Et. Despite the simplicity and obvious intuitive correctness of equation (1), the resulting price increases that are observed in real life tend to be higher compared with the excise tax increase, even if we will take into account the additional VAT augmentations, which are omitted from these formulas for the sake of simplicity. That means that the initial impression, that the final price is the sum of the costs augmented by the markup and excise tax Et may be wrong. For those periods when the prices go up at a higher rate compared with excise tax increments, the pricing equation looks much more like this:
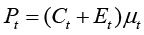 (2)
(2)
These two equations describe two ways for incorporating excise tax into the model. The first way adds excise tax as a certain add-on over the existing costs. If the excises are treated in this manner, the increase in excise tax has to lead to a proportional increase in the final price of the product. The second approach adds excise tax to the costs and multiplies it by the markup. This formulation may be incorrect in its essence, but allows to observe nonproportional price hikes, compared with the tax increments.
If the firms would base their pricing decisions upon the first formula, the prices would go up only by the amount of the excise tax, but if they would use the second approach, the increase in the price would be larger by the amount of markup. The usage of this approach leads to the increment in the final of the product that is larger than the change in the excise tax. Although simple, the second formula may be incorrect in an accounting sense, as the main reason why producers are increasing the price of a product at a higher rate, compared with the increment in the excise, may not be the result of a specific perception of excise taxes. As for the alcohol market, Young and Bielinska-Kwapisz, in their alcohol demand study, found that an increase in beer, spirits, and wine excise taxes lead to a rise in prices that is significantly larger than a rise in excise taxes (Young and Bielinska-Kwapisz, 2002). Therefore, we can more or less be sure that the majority of firms perceive excise taxes as in formula (1), as this is in accordance to the way accounting is done, but nonetheless the price after the revision is as if it was set by the formula (2). The main reason for this dichotomy lies in pricing policies that are used by companies and that result in what economists call “price stickiness.” Firms revise their prices, but they do it adhering to a certain regularity (Romer, 2011; Mankiw, 2018; Blinder, 1994). Hence, the periods when excise duties are raised provide a great opportunity to revise the prices. The question that we are dealing with in this paper is how excise taxes affect ethyl alcohol sales and how prices respond to the changes in excise taxes.
In order to address this research problem, we will (a) build a theoretical framework and (b) perform an empirical analysis in order to make sure whether the statements of the theoretical model are correct. An empirical model may also yield some additional interesting insights into the liquor market in Lithuania that are not covered by the theoretical model.
2. Model
Several conditions that cause these extra increases in the prices can be identified within the frames of a simple micro model. Pricing decisions are in the hands of producers, and they choose the price and quantity to maximize the profits. If we look at this a little more carefully, we will notice that pricing decisions are two-sided. The price consists of costs that are augmented by the markup; thus, price setting involves a wide spectrum of decisions regarding costs and markup. Markup is set above the costs; thus, the decisions regarding the markup follow the decisions regarding the level of costs. Costs and their particular structure determine the exact features of a product; thus, the costs specifically determine both the design and the final price of the product. In other words, costs are the key variable the manufacturers operate with in order to maximize their profits. In practice, the cost concept used here will match production costs only if it is a local manufacturer, but if it is an importer or seller of imported goods, costs will be associated with changes in assortment, when more expensive goods are replaced by cheaper ones.
The profit function, suitable for the taxation analysis, is a difference between sales revenues, costs, and excise taxes transfers, where income is defined as the price of unit multiplied by the quantity sold Qs,t, while the total cost is the product of costs per unit of production and quantity produced Qp,t:
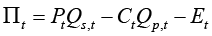 (3)
(3)
Specifying the exact structure of profits function, one has to be very specific regarding the costs, as income and expenditure levels are determined by different types of costs. The price, which is set for a particular period and is usually set ahead, depends not on actual, but on the expected sales and so on the expectsed costs per unit of production Ct*, so that:
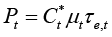 (4)
(4)
In this function, price is the product of expected costs of goods sold, of a markup and excise tax factor τe,t. The excise tax factor is defined so that Ct μt+Et=Ct μt τe,t; hence, it follows that τe,t = 1 + Et /(Ct μt). The costs that determine the price are related to the expected amount of goods sold, the expected prices of the raw materials, and so on, while the costs that determine the level of expenditures are related to the actual amount of goods produced and actual costs per unit of production, and so the equation (3) gets this form:
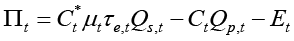 (5)
(5)
The difference between actual costs and their expected level should be minor under normal conditions, as the majority of producers know the prices of raw materials quite well and they usually set the price also taking into account minor, unexpected changes or fluctuations in labour, capital, or goods markets. This concept is fully compatible with the rational expectation hypothesis, which assumes that the difference between actual Ct and predicted Ct* levels of costs is a random error εc,t. In the multiplicative form, the rational expectation hypothesis states that:
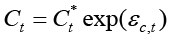 (6)
(6)
The second extension of profits function is related to income and is based on the plain and simple fact, that the amount of goods produced depends on the expected sales Q*s ,t:
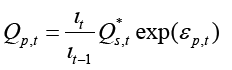 (7)
(7)
If the producers expect that in next periods they will face increases in demand, so in sales, they will expand the production. Specification of the exact relationship between actual quantity produced and expected sales has to take into account that production is a continuous process and the exact levels of production if this is a local producer, or plans for import of particular goods if this is an importer, are defined in organizations plans, which can be easily revised. For this reason, a certain fraction of a current year sales, usually these are the sales, that occur in the beginning of the year are the acquisition of goods that were produced in the final days or months of the preceding year. From the production perspective, we get the same impression: every year a certain fraction of goods, usually the production in final months and days of a certain financial period are produced for the needs of the subsequent periods. For the need to encompass these natural features of production continuity and planning regularity, we will define a new variable ιt, which is a specific factor of production that will be sold in the next period. If ratio of iotas ιt/ιt–1 on the longer run does not differ from unity, we are having a more or less stable production path. If the ratio exceeds unity on the short run, it means that producers are expecting the sales in period t +1 to go up, comparing with the sales in period t, and if the ratio is below unity, producers are expecting that the sales will decline. Let us assume that this ratio is equal to 1.05. This means that during the whole period in time, the demand has increased by five percent. If we will assume that this five percent increase was observed during the whole financial period, the ratio of iotas will be very similar to the prediction error. But if the influx of additional demand was observed only in the end of a financial period or in the beginning of it, this ratio will not represent the difference between the predicted sales and the actual level of production. For this reason, this ratio is multiplied by production error term exp(εp,t). As the production of majority of goods is a continuing process and the amounts of goods produced are usually revised, ιt/ιt–1 plays the role of correction factor, or, in other words, this ratio adjusts production volumes taking into account the differences between actual and predicted demand. In other words, it is a prediction error that manifests itself in the correction of inventories that will be left for the subsequent periods. Denoting ιt /ιt–1 exp(εp,t) as exp(ει,t) and applying this definition, the equation (7) expresses the current level of production as a deviation from expected sales:
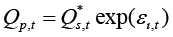 (8)
(8)
Quantity produced is a certain function of expected sales that is adjusted during the financial period, taking into account the new information, which has become available to manufacturers.
Assuming that agents are rational, actual costs differ from the expected – that is to say, from those that were expected when prices were set – only by the random error, that in the multiplicative form will be denoted as exp(εs,t), so that:
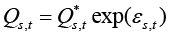 (9)
(9)
Substituting equations (6), (8), and (9) into equation (5) yields the following profits function:
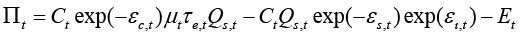 (10)
(10)
Quantity sold is the function of income and prices. In the usual microeconomic formulation, with a Cobb-Douglass style restriction, it may take this form:
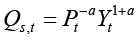 (11)
(11)
Equation (11) states that if price and nominal income will go up by one point, the demand will not change. Substituting equation (11) into (10) gives almost the final version of profits function:
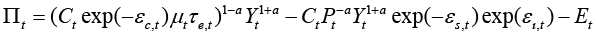 (12)
(12)
Prices that are on the right hand side of the equation depend on costs, so only substituting equations (4) and (6) into equation (12) yields the final version of profits function:
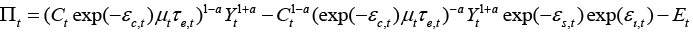 (13)
(13)
Costs are the main determinants of the product. Costs determine the main features of the product and the derivative of function (13) with respect to costs Ct, i.e., the first choice variable of the firm is:
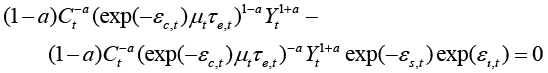 (14)
(14)
Dividing both sides of equation (14) by 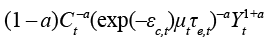 , gives the form, that can easily be solved for the markups, i.e., for the second choice variable:
, gives the form, that can easily be solved for the markups, i.e., for the second choice variable:
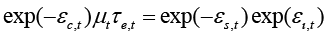 (15)
(15)
The amount added over the costs to cover the expenses and to guarantee the desirable level of profits is:
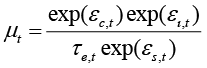 (16)
(16)
Markups are directly proportional to exp(εc,t), which is of no surprise, because if the actual costs exceed expected costs, the increase in markups is necessary to cover the unexpected profit losses. Markups are also directly proportional to the exp(ει,t) and exp(εs,t) ratio. From the equations (8) and (9), it follows that this ratio is a ratio of quantity produced to the ratio of quantity sold:
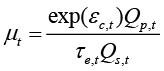 (17)
(17)
This equation implies that markups also tend to go up, when quantity produced exceeds quantity sold. This occurs when agents regularly overpredict demand and produce more goods than there are buyers for them. Producers overpredict demand in diminishing markets only if the fall in the demand is unforeseen. This may occur if there exists belief that decline will stop and will be reverted in the near future and if there exists certain burdens to compensate the diminished demand in one market with the increased sales in the other markets. If demand diminishes due to the declines in the number of buyers, the only remaining option that is left for the producers is to increase the price. Because of the very slow decline in population due to demographic changes, these markup increases are small and stretched over time.
If the sales are not to what they were expected, the only option to save profits from the fall is an increase in markup. As the producers will fear that such increase will call out a negative reaction from the consumers, they will try to find a pretext for the increase, and the decisions of the government to increase excise taxes may serve as good opportunity to disguise and mask the increases in markup.
Excise tax, on the contrary, has a negative effect on markups, as it causes additional increases in prices and forces the producers to lower the markup for the preservation of market share.
If excise taxes go up, while all other things stay the same, markups should diminish, or, in other words, prices should go up by a lower rate, compared with the increase in excises. But if in reality we observe the opposite, excise increases are followed by the extra increases in prices; this may be due to the misprediction of demand.
The increases in excise taxes may force the producers of local liquor and importers of ethyl alcohol to lower the costs of their products. In the case of the former, cost revision involves changes of the product specification, and for subsequent ones, cost revision will be associated with assortment changes, where more expensive products will be replaced by cheaper ones.
The problem with both options is that changing the product specification or changing the assortment will take time; thus, increases in excise duties will lead to a natural increase in markups. In subsequent periods, this increment may be offset by cost reductions or modifications in assortment.
In the short term after the excise increase, the markups are the only remaining option when it comes to the keeping of profits as not diminished as possible. So, the markups fluctuate in order to eliminate the effects of unforeseen long-run fluctuations on demand. Costs and markups are the main factors and sources in the hands of the firm that are used for the maximisation of profits. Costs determine the main features of a product, they determine the price level, the demand, and so on.
3. Empirical investigation of tax increments
In order to find out whether the statements of the theoretical model are consistent with reality and to obtain additional insights that complement the theoretical model, an empirical analysis of the data was carried out. For the empirical investigation of how tax increments affect alcohol sales, monthly data on alcohol sales and prices was used. The data sample used in the analysis ranges from January 2011 to January 2019.
3.1. Model for the sales of ethyl alcohol
The proper model building requires to distinguish between the changes in the market that are inevitable and have nothing to do with the object being directly modelled and those changes that are the result of direct and purposeful intervening into the market by administrative forces. When it comes to the analysis of particular goods markets in Lithuania, it should be noted that many markets in Lithuania are in a state of decline due to an objective reason – mass emigration that causes a decrease in the number of customers. Nelson conducted a study of alcohol demand in US and found that the decline of alcohol consumption was a result of the ageing US population and not a result of anti-drinking campaigns or price increases (Nelson, 1997). Therefore, an analysis of such markets should be based on sales per capita and not on the total sales of a particular product. In the context of alcoholic beverages, a per capita notion is not the best one, as not all members of the population are allowed to consume these products; thus, a much better choice would be to model the sales of alcohol per person who pass the legal drinking age. The variable of interest may be obtained taking the total amount of liquor sales and dividing it by the number of residents that pass the minimum legal drinking age requirement. The second motive behind this choice is that during the period being analysed, the minimum age for acquiring alcohol was changed. Thus, taking into account that the number of inhabitants in Lithuania is constantly decreasing and the minimum legal drinking age was raised on January 1, 2018, the proper variable for the sales are the sales per person who pass the legal drinking age requirements and not the total sales.
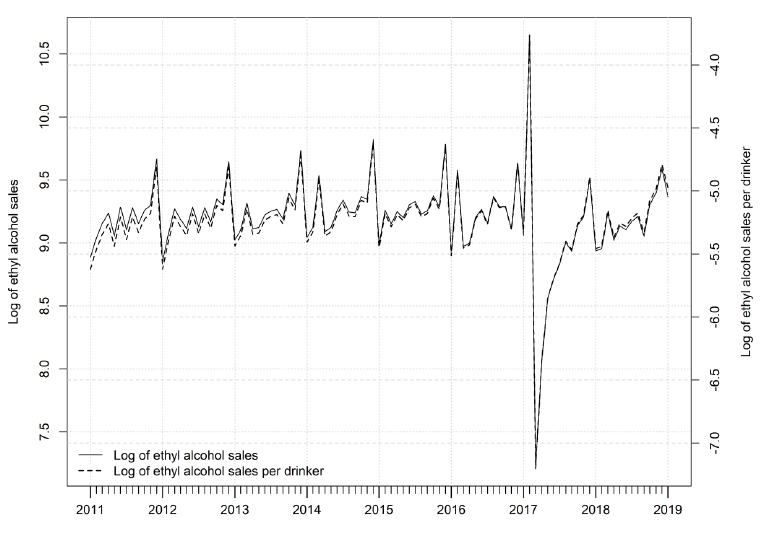
Fig. 1. Logarithm of total ethyl alcohol sales and sales per drinker in Lithuania in 2011M01:2019M01
Source: data provided by Lithuanian Business Confederation
Figure 1 presents the dynamics of both variables: total sales (solid line) and sales per person who pass the age requirement – sales per drinker (thicker dashed line). Glancing at the plot, one can easily note that the sales per drinker are slightly more stable than total sales and the tendency of slow decline is less visible.
After a long-lasting experiment, where all possible determinants of sales of spirits and liqueur per drinker qt have been assessed, the following model was obtained:
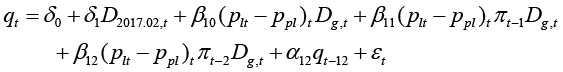 (18)
(18)
Here and further, πt stands for the growth rate of liquor prices in Lithuania, plt,t and ppl,t are logarithms of representative spirits and liquor prices in Lithuania and Poland respectively, so that the difference plt,t – ppl,t is the price gap or logarithm of price ratio. Dummy variable D2017.2,t takes unity for the February of 2017, when we observed abnormal increments in purchases of spirits, while dummy variable Dg,t takes unity for the periods when prices of spirits in Lithuania exceed the prices in Poland by more than 16.2 percent. Particularly this threshold was determined with the use of a simple iterative search rule, where all possible values for the threshold were used, but in the final stage, the one delivering the best fit of a model was chosen. The best fitting model yielded a potential break point of 0.15, which in a non-logarithmic form is 1.161834 and which in itself means that the demand for ethyl alcohol in Lithuania negatively reacts to the price difference between Lithuania and Poland only when prices in Lithuania exceed Polish prices by more than 16 percent.
Alcohol consumption is culturally determined and that determination affects not only volumes or frequency of consumption, but also preferences for certain types of beverages or preferences for certain producers, e.g., local over non-local. This threshold identifies the price gap between Lithuania and Poland, when locals (Lithuanians) start to show preferences for non-local (made in Poland or sold in Poland) products. Consumers prefer domestic over the non-local only up to a certain point – when the price level of local products exceeds the prices of non-local products by 16 percent, consumers start to show preferences for imported products over non-local products. The estimates of coefficients of equation (18), their standard errors and their t values are provided in table 1.
Table 1. The estimates of demand equation (18)
|
Variables / Coefficients |
Estimate |
Std. |
t value |
p value |
|
Intercept δ0 |
-5.1914 |
0.0385 |
-134.8627 |
< 0.0001 |
|
Dummy for the 2017M02 δ1 |
1.3944 |
0.2009 |
6.9404 |
< 0.0001 |
|
Product of the price gap and gap dummy β10 |
-1.9616 |
0.5237 |
-3.7454 |
< 0.0002 |
|
Product of the price gap with the 1st lag of the growth rates of liquor prices and gap dummy β11 |
-0.5586 |
0.1474 |
-3.7894 |
< 0.0002 |
|
Product of the price gap with the 2nd lag of the growth rates of liquor prices and gap dummy β12 |
-0.5471 |
0.1532 |
-3.5701 |
< 0.0004 |
|
12th autoregressive coefficient α12 |
0.4499 |
0.0967 |
4.6538 |
< 0.0001 |
Source: author’s calculations, using Eurostat’s and Lithuanian Business Confederation data
For the sake of curiosity it can be mentioned that quasi r-squared for this model is around 0.6, residuals act as white noise, are un-autocorrelated, homoscedastic, and linear. In the initial versions of the model, the heteroskedasticity of errors and the obvious signs of nonlinearity served as the main tools for the creation of the final version of the model.
This model implies that if prices in Lithuania do not exceed Polish prices by more than 16 percent, demand is purely autoregressive, the price is inelastic and displays regular seasonal fluctuations as implied by the 12th lag of sales, which is present in the model:
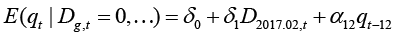 (19)
(19)
This conditional expectation of the function (18) defines the demand function for the periods when prices in Lithuania do not differ very much from the prices that exist in Poland, i.e., when prices in Lithuania do not exceed prices in Poland by more than 16 percent. Setting dummy Dg,t to unity and then taking conditional expectations of equation (18) yields a demand function for the periods when prices in Lithuania exceed prices in Poland by more than 16 percent:
 (20)
(20)
Under these conditions, demand is already price elastic. The fact that demand in Lithuania responds to certain external factors only when the gap is at least somewhat noticeable (in our case, it is around 16 percent) should not be surprising. The shopping journeys of Lithuanians to Poland are costly (uppermost fuel and time) – hence, the prices in Poland have to be significantly lower than in Lithuania for Polish products to become substitutes for Lithuanian ones. This is the necessary condition for Lithuanian products to be substituted by analogous Polish goods. It is the existence and availability of substitutes that makes the demand of alcohol price elastic.
This paragraph of the article is the best place to discuss the two nuances that are present in the empirical model: cross-border shopping and the elasticity of demand with respect to prices. Cross-border shopping is a widely known phenomenon and for border zone inhabitants it is a daily routine. Some of cross-border alco-shopping episodes have already made history, and one of them is described in the study conducted by Nordblom: “since Sweden joined the EU in 1995, the cross-border shopping has radically increased due to the considerably lower excise duties on alcoholic beverages in other EU countries” (Nordblom, 2011). Asplund, Friberg, and Wilander also used Swedish data to model the effects of Danish tax cuts on the sales and tax revenues in Sweden (Asplund et al., 2007). Thus, these are few examples when lower excise duties in one country attract consumers from another.
When it comes to alcohol, the elasticity of demand with respect to prices is seen as something that is controversial. Quek was one of the pioneers who conducted a detailed econometric study of the elasticity of alcohol demand to prices and income and found that elasticities are not constant – they change over time (Quek, 1988). There are plenty of articles the authors of whom, like Quek, recognize that the elasticity of demand for alcohol varies over time; however, there are much more of those authors who limit themselves to the estimation of point elasticities for a particular period in time; e.g., Selvanathan found that in eight OECD countries, the elasticity of alcohol demand with respect to prices is around –0.6 (Selvanathan, 2006) and for separate alcohol groups elasticities are –0.2 for beer, –0.3, for wine, and –0.6 for spirits (Clements and Selvanathan, 1991). Andrikopoulos and Loizides calculated elasticities for various alcohol products and found that the highest elasticity is for imported beer –0.9976, while the lowest is for home-produced brandies, which is –0.1734 (Andrikopoulos and Loizides, 2000). And there are many more articles like these. Of course robust constant point estimates for a particular period give a good retrospective assessment; however, they are of little use if the conditions that are responsible for the shifts in the magnitudes of the coefficient suddenly change. The fact that elasticities are not constant and time-dependent is not surprising. It is rather an indication that the disclosure of the factors driving these changes will require to apply nonlinear modelling tools.
Studies of alcohol demand elasticities can be divided into two blocks – micro and macro studies. Micro-scale studies provide huge amount of evidence of alcohol demand elasticity, e.g., in the study done by Durrance, Golden, Perreira and Cook, the authors conclude that alcohol taxes may reduce alcohol consumption for individuals who are most sensitive to prices (Durrance et al., 2011). Chaloupka, Grossman and Saffer found that higher alcohol taxes lead to the reduction of alcohol consumption among youths and young adults (Chaloupka et al., 2002). This micro-level study asserts that some individuals will reduce their consumption as prices rise, but some other individuals, who are not sensitive to the changes in the prices, will not revise their consumption even if prices go up. If the proportion of individuals in the first group is small across the whole society, consumption will not be very price elastic on a macro scale. On the other hand, under certain conditions, the individuals whose consumption was inelastic to prices may suddenly become price elastic. Thus, on a macro scale, the picture may be slightly different and may reveal macro-factors that influence the consumption of individual groups without distinguishing the groups themselves.
Of course when it comes to macro-scale studies, the conditions that are responsible for the changes in elasticities are much more important than the extent of elasticity itself. As for the extent of elasticity itself, the claims that alcohol demand is price inelastic may sound radical, but even this may be true under certain conditions (Nelson, 1997). Unlike the Quek or similar studies, this article demonstrates under what conditions demand is inelastic and how its elasticity forms and changes. These conditions are clearly defined in equation (18), which turns to a pure autoregression where demand does not respond to prices at all, if prices in Lithuania are similar to those that exist in Poland (equation (19)) and to a specific nonlinear model (equation (20)), when Poland becomes a significantly cheaper place to shop at than the home country. The estimates reveal that under this setting, alcohol demand responds to the changes in the price gap between Poland and Lithuania and to the overall growth rate of liquor prices observed in Lithuania.
This demand function contains two nonlinear responses, both of which occur only when prices in Lithuania are significantly higher than the prices in Poland, i.e., only while the substitution effect is in effect. The first of these responses can be identified by taking the derivative of demand equation (18) with respect to price gap:
 (21)
(21)
The response of demand onto the changes in price ratio is the derivative of demand with respect to price gap. This derivative is itself a function of the growth rates of liquor prices; thus, the response of demand with respect to the price gap depends on the growth rates of liquor prices in the previous two months.
Fig. 2. The response of local sales to the price gap between Poland and Lithuania
Source: author’s calculations
Figure 2 depicts all possible responses of local sales in Lithuania onto the change in the Lithuanian and Polish price gap for various growth rates of liquor prices in Lithuania (starting with 0.5 percent decrease in the prices and ending up with 2 percent increase). If the price gap goes up by one percentage point and if in the previous two months we have observed the growth of ethyl alcohol prices equal to one percent, this will lead to the reduction of ethyl alcohol demand by 2.5 percentage points. If the growth rates for liquor will account for 1 percent in the last two months, the demand for ethyl alcohol will go down by 3 percentage points; 1.5 and 2 percentage point increases in the growth rates for liquor product prices will result in 3.6 and 4.2 percentage point declines in demand.
The fact that sales in Lithuania are more dependent on the price difference between Poland and Lithuania than on prices in Lithuania gives reason to suspect that Lithuanian consumers are choosing Poland instead of Lithuania to buy ethyl alcohol.
The second of the two nonlinear responses is obtained by finding the derivative of demand function (18) with respect to liquor inflation:
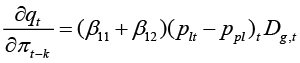 (22)
(22)
This derivative is itself a function of the price gap that exists between Poland and Lithuania; thus, the strength of a particular demand response on changes in the prices depends on the price difference that exists between Poland and Lithuania.
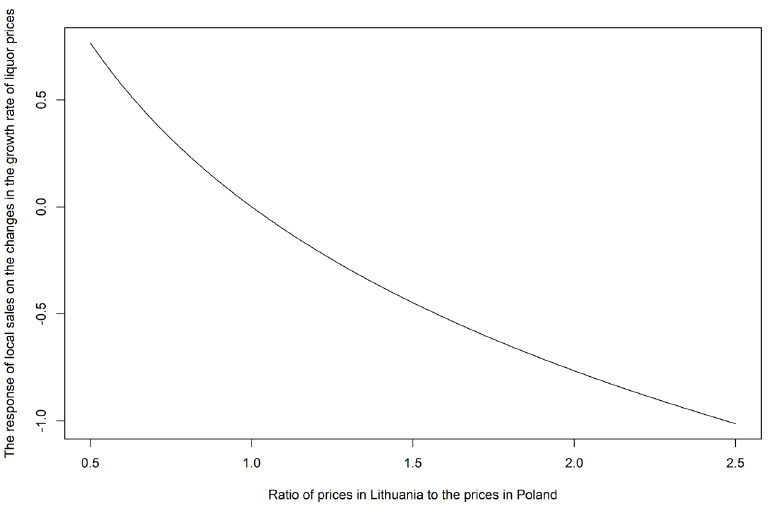
Fig. 3. The response of local sales to the changes in the growth rate of liquor prices
Source: author’s calculations
Figure 3 depicts all possible responses of local sales in Lithuania onto the growth rate of liquor prices, for the various levels of liquor inflation (starting with 0.5 percent decrease in the prices and ending up with 2 percent increase).
If the growth rate of price goes up by one percentage point two months in a row and if Lithuanian prices account for 90 percent of Polish prices, no reductions in demand will be observed – it is even possible that demand will go up by 0.12 percentage points. If prices in Lithuania and Poland are equal, the change in the growth rate of the prices will not have any effect on demand at all, but if prices in Lithuania exceed prices in Poland, demand starts to react negatively on the changes in the growth rate of the prices. Thus, in the ethyl alcohol market, the elasticity of demand with respect to prices exists and is determined by the availability of substitutes. When there are no cheaper alternatives to buy liquor, demand does not respond to the changes in the prices or responds in a completely different direction, because rising prices may form the expectations of further increases and so businesses and individual consumers may increase purchases in order to acquire alcohol at the lowest price as possible. A completely different situation is observed when Lithuanians have a choice to acquire alcohol at a lower price in Poland. The cheaper Polish products become, the more eager Lithuanians will become to substitute locally sold liquor with the liquor sold in Poland. This is how the effect of substitution arises. When prices in Lithuania exceed prices in Poland by 20 percent, demand goes down by 0.2 percentage point if prices go up. This effect of negative elasticity becomes more visible every time the gap between Lithuania and Poland increases. When prices in Lithuania exceed prices in Poland by 50 percent, demand goes down already by 0.45 percentage point, responding to the increases in local prices. Every time the excise taxes in Lithuania were raised, the effect of low-priced Poland became more visible, and with every subsequent increase, the demand became more and more elastic to the prices. Increases in excise taxes, disregarding the level of excise that exists in neighbouring countries, creates the opportunity for local consumers to take advantage of the substitution effect.
3.2. Model for the growth rate of ethyl alcohol prices
The supply side is defined by the ethyl alcohol inflation variable. The main reason for choosing inflation and not the prices is that price level cannot be treated as a stationary variable in any way; thus, the only remaining option is to use its stationary counterpart – the growth rate of the prices.
Fig. 4. Log of ethyl alcohol prices and their growth rates in Lithuania in the period of 2011M01:2019M12
Source: Eurostat’s data on Lithuanian economy
A careful inspection of the prices reveals that prices tend to go up immediately after the excise taxes were raised, but later, over a period of three to six months, they fell backwards. These dynamics are fully in line with the theoretical model, which foresees the opportunity to review the costs for manufacturers or to change the range of products for importers, replacing more expensive products with cheaper ones. The dynamics of price curve indicate that as a result of the increase in excise duties, mark-ups initially increase and then go down. What is not clear yet is what determines these fluctuations.
The liquor inflation curve (a thicker dashed line in figure 4) displays significant volatility patterns, and the blind application of econometric modelling tools would suggest the estimation of a certain GARCH model. However, such a choice would be wrong, as the volatility pattern in this series is the result of excise tax increases that occurred on April 2014, April 2015, March 2016, and March 2017, when with each successive increase in excise duties, the volatility of inflation went up. The GARCH model could be applicable only and only if the volatility would have been the result of inflation shocks that represent unexpected changes in price hikes. In our case, all volatility hikes are the result of cabinet decisions made by the government and parliament officials. These decisions have been announced to the public in advance, so they were fully predictable and thus they cannot be treated as effects of purely random factors, and thus the GARCH model cannot be applied here.
However, heteroskedasticity models are more frequently used to model financial variables, while in macro- or microeconomic models the same properties of a variable can be modelled using a non-linear approach; thus, it should not be a big surprise that the final model for liquor inflation will be a specific nonlinear model. The initial draft of the model contained all necessary lags of liquor inflation in order to model inertia and four dummies that were used to model changes in excise tax levels, which occurred on April 2014, April 2015, March 2016, and March 2017. The initial draft of the model had un-autocorrelated errors, but their squares displayed several significant autocorrelations, which should not be of a big surprise as the graph of liquor inflation in figure 4 displays obvious signs of volatility. One of the reasons why this tendency should not be approached directly is choice of a simple GARCH model, which was explained above, but the main reason for not following the heteroscedasticity modelling path is that increased volatility or autocorrelation of the squares is a feature that is present when the response of a variable onto a certain factor depends on the level of this factor or onto the level of a certain other variable. The response of the growth rate of alcohol prices onto the changes in demand may depend on the level of demand itself or onto some other factors; thus, in this case, the suitable tool for the estimation of interdependencies should be a certain nonlinear autoregressive model.
The demand factor that was defined in the theoretical model and the price difference between Lithuania and Poland, the importance of which is determined by a very large number of Lithuanian customers that regularly visit Poland for shopping purposes, were included only in the second phase of the model search. Price difference is a very important factor and although it is not included in the theoretical model, its importance is indisputable. This difference in a certain way represents the substitution element for local sales; because of the very large number of visitors from Lithuania, liquor sold in Poland is a substitute for liquor sold in Lithuania.
The final version of the model, with properly modelled nonlinearities and a purely random error term, takes this form:
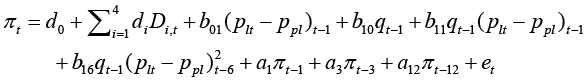 (23)
(23)
The pricing equation (23) already satisfies all statistical requirements regarding residuals being white noise, conditionally homoscedastic, and linear. In this equation, four dummy variables D1,t, D2,t, D3,t, and D4,t are used to model the changes in the levels of excise taxes that occurred on April 2014, April 2015, March 2016, and March 2017, while the remaining variables were introduced and discussed earlier. The structure of model (23) implies two nonlinear responses of liquor inflation on the changes in demand and price gap. Quasi r-squared for this model as for the model (18) is also around 0.6 and the residuals are in all respects purely random. In the initial settings, the errors were highly nonlinear and heteroscedastic in the initial versions of the model; however, after the inclusion of suitable nonlinear factors, problems have been resolved. The estimates of coefficients, their standard errors, and their t values are provided in table 2.
Table 2. The estimates of pricing equation (23)
|
Variables / Coefficients |
Estimate |
Std. Error |
t value |
p value |
|
Intercept d0 |
0.2849 |
0.0675 |
4.2206 |
< 0.0001 |
|
Dummy for the excise increases in 2014M04 d1 |
-0.0097 |
0.0039 |
-2.5160 |
0.0119 |
|
Dummy for the excise increases in 2015M04 d2 |
-0.0059 |
0.0034 |
-1.7150 |
0.0863 |
|
Dummy for the excise increases in 2016M03 d3 |
0.0078 |
0.0039 |
1.9861 |
0.0470 |
|
Dummy for the excise increases in 2017M03 d4 |
0.0213 |
0.0067 |
3.1826 |
0.0015 |
|
1st lag of Lithuanian and Polish price gap b01 |
-1.9561 |
0.4494 |
-4.3526 |
< 0.0001 |
|
1st lag of quantity sold b10 |
0.0515 |
0.0132 |
3.8988 |
0.0001 |
|
Product of the 1st lag of sales and of 1st lag of price gap b11 |
-0.3380 |
0.0875 |
-3.8609 |
0.0001 |
|
Product of the 1st lag of sales and 6th lag of price gap squared b16 |
0.1109 |
0.0507 |
2.1858 |
0.0288 |
|
1st autoregressive coefficient a1 |
-0.1529 |
0.0834 |
-1.8337 |
0.0667 |
|
3rd autoregressive coefficient a3 |
-0.2074 |
0.1015 |
-2.0435 |
0.0410 |
|
12th autoregressive coefficient a12 |
0.4638 |
0.1114 |
4.1650 |
< 0.0001 |
Source: author’s calculations, using Eurostat’s and Lithuanian Business Confederation data
The estimates of the coefficients reveal that if demand goes up, prices also tend to go up, but the overall rate of price increases is determined and formed by the Polish and Lithuanian price gap. When prices in Lithuania are lower than prices in Poland, increases in demand tend to fuel up the growth rate of the prices, and on the other hand, when Lithuanian prices exceed Polish prices, demand increases are associated with more moderate growth rates of liquor prices.
The response of the growth rate of liquor prices onto the changes in demand is the derivative of pricing equation (23) with respect to the first lag of quantity sold:
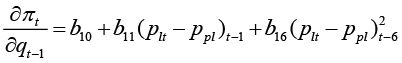 (24)
(24)
Taking the growth rate of the prices as a response, it is clear that the response of inflation onto the changes in demand depend on the difference between prices in Lithuania and Poland. The growth rate of alcohol prices also tend to respond to the changes in demand. The response is not immediate but nevertheless very fast – the changes in demand cause the changes in pricing in approximately one month. The magnitude of the response is non-linearly dependent on the price gap, which exists between Lithuania and Poland. The estimates reveal that if the price level in Lithuania will amount for 90 percent of the Polish price level, the increase in demand will result in an additional price hike – the producers, importers, and the sellers of liquor products will not resist the temptation to increase the price of a marketable product that costs more in the neighbouring country.
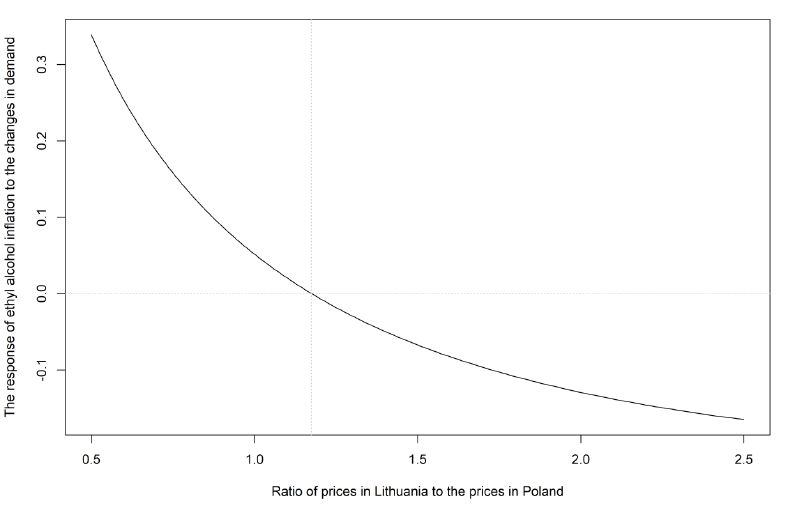
Fig. 5. The response of ethyl alcohol inflation to the changes in demand
Source: author’s calculations
Figure 5 contains the graphical representation of how the growth rate of the prices responds to the changes in demand at various levels of price differences between Lithuania and Poland. The positive response of the growth rate of prices to the changes in demand declines when the negative gap between Lithuanian and Polish prices decreases and when prices in Lithuania tend to overcome Polish prices. If Polish prices exceed Lithuanian ones by 20 percent, and this increase is present for about half a year, the growth rates of alcohol prices will increase by 0.13 percentage points. On the other hand, if Lithuanian prices exceed Polish prices 1.5 times, the growth rate of alcohol prices will decline by 0.07 percentage point, even when demand is on the rise. Overall, the higher the price gap between Poland and Lithuania is, the lower the price hikes will be, even when demand is growing.
The second nonlinear response is associated with the response of the growth rate of the prices onto the price gap that existed in the near past. The exact mathematical expression of this response can be obtained by finding the derivative of the pricing function (23) with respect to price gap:
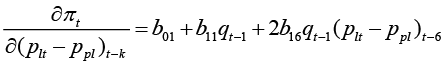 (25)
(25)
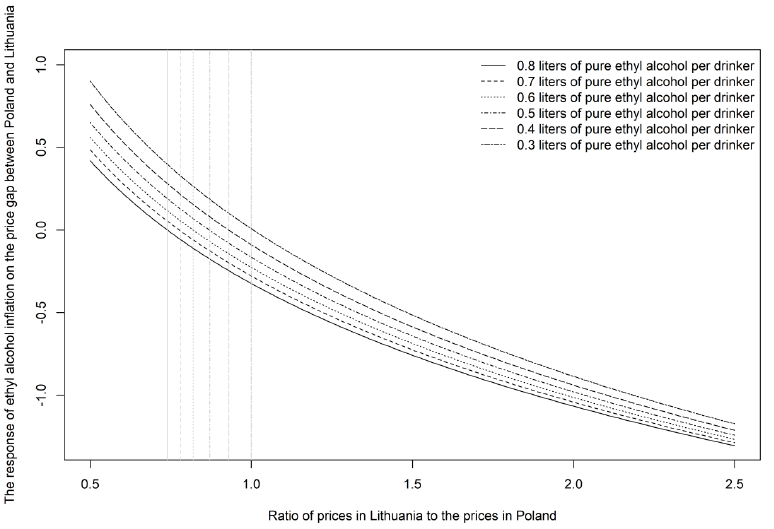
FIG. 6: The response of ethyl alcohol inflation to the price gap between Poland and Lithuania
Source: author’s calculations
Figure 6 contains responses of liquor inflation to the changes in price gap, for various levels of sales per drinker, starting with 0.3 litres of pure alcohol per head and ending up with 0.8 litres of pure alcohol per head. The response of liquor inflation on the price gap depends on demand and on the price gap that existed half a year ago. If the amount of ethyl alcohol sales is quite low and accounts for 0.3 litres of pure alcohol per drinker in a month (two-dashed line in figure 6), the growth rate of price will start to slow down, when prices in Lithuania will start to exceed prices in Poland. If alcohol sales per drinker are higher, the response of the growth rate of local prices changes its nature much quicker. When the amount of ethyl alcohol accounts for 0.4 litres per drinker in a month (long-dashed line in figure 6), the growth rate of local prices will start to decline when prices in Lithuania will exceed 93 percent of the prices in Poland. At the level of 0.5 litres per drinker (dot-dashed line in figure 6), this threshold is at 87 percent, and at the levels of 0.6, 0.7, and 0.8 litres per drinker (dotted, dashed and solid lines in figure 6), the thresholds are correspondingly at 82, 78, and 74 percent of the prices in Poland. Thresholds for various levels of liquor sales are denoted in the figure 6 as vertical light grey lines of the same type as the main lines are.
Summing up the inflation equation, we can state that initial increase in the prices is fully influenced by the increase in excise duties, while the subsequent price level adjustments are the result of reductions in demand for domestically sold liquor and increases in demand for low-priced goods in Poland (the aforementioned substitution effect). The downward response of local prices, which resulted from changes in costs (revision of assortment and possibly manufacturing costs) or from downward changes in markups, caused a recovery of sales.
4. Concluding remarks
The theoretical model that is presented in the first half of the article states that excise taxes have a negative effect on the markups. The increase in excise taxes raises the prices immediately, which in competitive markets causes the reduction in demand. Thus, in order to offset the losses from the diminished demand, producers and importers of liquor will lower the costs and revise the assortment of goods, replacing more expensive goods and ingredients with cheaper ones. After a while, such decisions lead to a fall in the price level and to the recovery of sales, but with lower markups. Of course, there is also the possibility to reduce only the markup.
Alcohol sales are price-elastic, but elasticity depends on the price difference between Lithuania and Poland. The price gap between Lithuania and Poland is a major determinant of sales and price dynamics. If prices in Lithuania do not differ very much from the prices in Poland, alcohol sales are not price elastic, but if prices in Lithuania exceed Polish prices by more than 16 percent, elasticity becomes noticeable. Almost all the time until March 2017, excise duties in Lithuania did not differ very much from those in Poland, so there was no significant price difference between the two countries, and the supply in Polish stores could not be considered as a substitute for the products sold in Lithuania. The increase in excise duties in March 2017 raised prices in Lithuania and caused the products sold in Poland to become substitutes for the products sold in Lithuania. The existence of the Polish substitution effect, in turn, created incentives for Lithuanian producers and importers to review the range of imported products, replacing more expensive products with cheaper ones, and to revise the costs of some local products. This, in turn, led to a drop in prices that was observed three to six months after the excise taxes were raised and caused a consequent recovery of the ethyl alcohol demand.
These findings are in line with the results presented in other studies. Andrienko and Nemtsov carried out their own research of alcohol preferences and found that increases in prices leads to reduction in consumption. This conclusion seems to imply that price increases will lead to the decreases in alcohol consumption, but the authors themselves note, that there is a strong substitution effect by other types of drink (Andrienko and Nemtsov, 2006). Thus, the price increase for one of the beverage categories leads to an increase in demand for the other alcohol categories. The same is true for small Lithuania, where the rise in prices, due to the increase in excise duty, creates a Polish substitution effect.
Consumers in Lithuania, just like anywhere else, prefer domestic over the non-local products only up to a certain point – when the price level of local products exceeds the prices of nonlocal products by 16 percent, consumers start to show preferences for imported products over non-local products. Hence, the increase in excise duties creates competition with goods from those neighbouring European Community countries where excise duties are significantly lower and which are frequently visited by a significant proportion of the population of the country.
The responses in empirical models of demand and prices are nonlinear and depend on various external factors. The response of sales onto the price gap between Poland and Lithuania depends on the observed growth rates of ethyl alcohol prices in the recent past. If the relative price gap already accounts for 16 or more percent, every subsequent increase in price will lower local demand. Under this condition, huger increases in the growth rates of the prices tend to cause significant declines in local demand for liquor.
On the other hand, the strength and magnitude of a particular demand response on the changes in the growth rate of Lithuanian prices depends on the price difference that exists between Poland and Lithuania. The increases in Lithuanian excise taxes created the effect of low-priced Poland, and this effect became more and more visible with every subsequent increase, causing liquor demand to become more and more elastic to the prices.
The analysis of the supply side revealed that the growth rate of the liquor prices responds to the changes in demand, but the magnitude and the size of the responses are non-linearly dependent on the difference between prices in Lithuania and Poland. The positive response of the growth rate of prices to the changes in demand declines when prices in Lithuania tend to catch up and overcome Polish prices. The higher the price gap between Lithuania and Poland is, the lower the price hikes will be, even when demand is growing.
Local liquor inflation is also dependent on the changes in the price gap; however, this relationship depends on the level of demand and on the price gap that existed in the near past. If alcohol sales per drinker are higher, the response of the growth rate of local prices changes its nature much quicker – the higher the difference between the prices in Poland and Lithuania is and the higher sales are, the quicker and more visible reduction in prices will be observed.
In conclusion, increases in excise duties lead to price increases, which lead to the emergence of competition between Poland and Lithuania. Higher excise taxes create a substitution effect, which forces domestic producers and importers to reduce prices by changing the assortment of imported goods or certain characteristics of locally produced goods, or to lower the markups. These actions lead to the restoration of sales after a while.
References
Andrienko Y., Nemtsov A. (2006). Estimation of Individual Demand for Alcohol. Working Papers w0089, Center for Economic and Financial Research (CEFIR).
Andrikopoulos, A., Loizides, J. (2000). The demand for home-produced and imported alcoholic beverages in Cyprus: the AIDS approach. Applied Economics, 32, pp. 1111–1119, https://doi.org/10.1080/000368400404254
Asplund, M., Friberg, R., Wilander, F. (2007). Demand and distance: evidence on cross-border shopping. Journal of Public Economics, 91, pp. 141–157, https://doi.org/10.1016/j.jpubeco.2006.05.006.
Blinder, A.S. (1994). On Sticky Prices: Academic Theories Meet the Real World, in Mankiw, N.G. (Ed.), Monetary Policy. University of Chicago Press, pp. 117–154.
Chaloupka, F.J., Grossman, M., Saffer, H. (2002). The effects of price on alcohol consumption and alcohol-related problems. Alcohol Research & Health, 26(1), pp. 22–35, https://doi.org/10.3386/w4385.
Clements, K.W., Selvanathan, S. (1991). The economic determinants of alcohol consumption. Australian Journal of Agricultural Economics, 35(2), pp. 209–231, https://doi.org/10.1111/j.1467-8489.1991.tb00506.x.
Durrance, C.P., Golden, S., Perreira, K., Cook, P. (2011). Taxing sin and saving lives: Can alcohol taxation reduce female homicides? Social Science & Medicine, 73(1), pp. 169–176, https://doi.org/10.1016/j.socscimed.2011.04.027.
Karpuškienė, V., Rastenienė, A., Liepuonius, A. (2019). Alkoholio vartojimo įpročiai, aplinka ir pasekmės Lietuvoje. Socialinė teorija, empirija, politika ir praktika, 18, pp. 59–73, https://doi.org/10.15388/stepp.2019.4.
Mankiw, N.G. (2018). Macroeconomics, tenth ed. Worth Publishers, New York. Result score too low
Nelson, J.P. (1997). Economic and Demographic Factors in U.S. Alcohol Demand: A Growth-Accounting Analysis. Empirical Economics, 22(1), pp. 83–102, https://doi.org/10.1007/bf01188171.
Nordblom, K. (2011). The complex attitudes to alcohol taxation. Applied Economics, 43, pp. 3355-3364, https://doi.org/10.1080/00036841003636276 .
Quek K.E. (1988). The demand for Alcohol in Canada: An econometric Study. Discussion Paper No. 88.08, Department of Economics, The University of Western Australia.
Romer, D.H. (2011). Advanced Macroeconomics, fourth ed. McGraw-Hill/Irwin, New York.
Selvanathan, S. (2006). How similar are alcohol drinkers? International evidence. Applied Economics, 38, pp. 1353–1362, https://doi.org/10.1080/00036840500396780.
Young, D., Bielinska-Kwapisz, A. (2002). Alcohol Taxes and Beverage Prices. National Tax Journal, LV(1), pp. 57–73, https://doi.org/10.17310/ntj.2002.1.04.