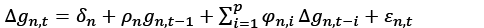 (1)
(1)Ekonomika ISSN 1392-1258 eISSN 2424-6166
2023, vol. 102(1), pp. 26–40 DOI: https://doi.org/10.15388/Ekon.2023.102.1.2
Göksel Karaş*
Assist. Prof., Department of International Trade and Finance,
Kutahya Dumlupinar University, Kutahya, Turkiye
E mail: goksel.karas@dpu.edu.tr
https://orcid.org/0000-0003-4091-1258
Ebru Karaş
Res. Assist. Dr., Department of Public Finance, Usak University, Usak, Turkiye
E mail: ebru.cilli@usak.edu.tr
https://orcid.org/0000-0003-0625-3722
Abstract. The presence of convergence in the fiscal policies implemented at the national level to eliminate regional disparities is an indication that the resources are rationally distributed among the regions, and the disparities are decreasing. From this point of view, this study aims to investigate the convergence of the fiscal policy implemented in the period of 2004:01–2020:12 in Turkiye within the scope of the fiscal aim of taxes. The research methodology includes the evaluation of structural convergence between regions in Turkiye to reveal similar and different aspects of fiscal aim through the Panel Threshold Unit Root Test (Panel TAR) and Evans–Karras linearity convergence test. In the study, nonlinear convergence analysis was performed, but linear convergence analysis was used because the linearity hypothesis could not be rejected. According to the findings, there is an absolute convergence among the regions in the fiscal policy implemented in Turkiye. However, in terms of regions, the first region is differentiated from the other five regions, while the other regions are very close to each other. Regarding this, it may be possible to bring the first region and the other five regions closer to each other by reducing the disparity in the arrangements made in taxation policies. It should be aimed that each region has a comparative advantage according to its characteristics by implementing an effective policy to eliminate the disparities between regions.
Keywords: convergence, fiscal aim, fiscal policy, region, Turkiye.
___________
* Corresponding author
Acknowledgements. This study was supported by Kutahya Dumlupinar University Scientific Research Projects Unit within the scope of project number 2022-07.
Received: 12/05/2022. Revised: 20/01/2023. Accepted: 08/02/2023
Copyright © 2023 Göksel Karaş, Ebru Karaş. Published by Vilnius University Press
This is an Open Access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
The study aims to investigate the existence of convergence in Turkiye in the period of 2004:01–2020:12, taking into account the fiscal aim of taxes based on incentive regions. The primary objective of the states is to ensure the equilibrium between public expenditures and revenues. At this point, public expenditures are financed by public revenues as a fiscal aim. The study investigates whether there is a convergence among regions in the country to achieve the fiscal aim. Budget deficits are among governments’ most critical problems, especially with the Covid-19 pandemic. The budget deficit problem started with the 2008 global financial crisis and deepened with the Covid pandemic that emerged in 2019 (Rompuy, 2021; Tevdovski et al., 2021). One of the main reasons for the emergence of this problem is the increase in public expenditures. The increase in public expenditures is due to the social and economic functions undertaken by the states. At the same time, the mentioned crises and global developments may also cause an increase in the public expenditures of the countries. The idea that the state should intervene in the economy, advocated by the Keynesian view, and that the economy should be operative instead of budget balance may also cause an increase in public expenditures and, thus, budget deficits over time (Terra et al., 2021).
States use several instruments to achieve their fiscal policy aims. These instruments include public expenditures and tax revenues. One of the fiscal policy’s most essential aims is eliminating national and regional development disparities. This aim, which expresses the role of the state in eliminating regional disparities, affects the regional distribution of the public budget, that is, the distribution of public expenditures and tax revenues among regions (Dökmen and Tekbaş, 2011). States use fiscal policy instruments effectively to eliminate total disparities. While more public expenditure is made in less developed regions, there is a tendency to collect fewer taxes. In this way, economic activities are tried to be encouraged in underdeveloped regions. This situation may lead to a budget deficit by causing public expenditures to be higher than tax revenues in less developed regions. The highest contribution to the budget deficit reduction is made by the developed and highly industrialised regions. From this perspective, the evolution of fiscal policy across the country and among regions is essential for various macroeconomic objectives such as development, growth, and investment (Apergis and Cooray, 2014).
To reduce the budget deficit, tax revenues must be either higher than public expenditures or at least as much as public expenditures. In other words, tax revenues should provide financing for public expenditures. This situation expresses the fiscal aim of taxes. Investigating the convergence of fiscal policies implemented among regions within the scope of fiscal aim can help policymakers to evaluate the fiscal policy implemented (Apergis, 2015). Convergence is a situation where the fiscal aim is realised similarly among regions. The absence of regional convergence in policies helps policymakers to implement policy measures that encourage the integration of fiscal policy (Apergis and Cooray, 2014). In addition, investigating the convergence of public expenditures and tax revenues among regions within the scope of fiscal aim can be a guide in terms of preventing the burden on some regions at the point of budget balance and preventing the exploitation of public resources by regions with the flexibility (Winner, 2005).
The convergence of tax revenues and public expenditures among regions can be used as an indicator of whether there is a rational distribution of resources among regions due to the implementation of a series of fiscal policies (Apergis, 2015). The rationale behind fiscal policy convergence is based on two critical approaches. The first of these is the classical view. According to classical theory, fiscal policy is not effective on economic activity in the long run. For this reason, public expenditures and tax revenues should be as low as possible (Tanzi, 2005). The resources used by the public sector are considered to be wasted in terms of the economy as a whole, and it is stated that these resources are used for the consumption of people who do not contribute to production (Smith, 1977). According to the classical view, a balanced budget policy should be followed by keeping public expenditures and tax revenues to a minimum. However, the global financial crisis experienced in 2008 revealed the importance of fiscal policy and showed that fiscal policy could impact potential output (Apergis, 2015). The second is the Keynesian view. According to the Keynesian theory, initially, less developed regions are encouraged to spend more and collect fewer taxes within the scope of fiscal policy. Thus, in the long run, it is expected that the fiscal policy will converge throughout the country (Apergis, 2015). The Keynesian theory was put forward in the world based on the lessons learned in the Great Depression of 1929. Accordingly, while monetary policy is effective in stopping price increases, it is stated that it is not sufficient to stimulate the economy in case of unemployment. At this point, the effectiveness of fiscal policy is emphasised. According to the Keynesian view, the effectiveness of the fiscal policy on national income is explained through the multiplier mechanism (Tokatlıoğlu and Selen, 2019). Fiscal policy convergence is significant for countries achieving primary macroeconomic objectives such as economic growth and development. Therefore, the convergence of fiscal policies among regions in the country is essential for policymakers and macroeconomic targets.
When the studies in the literature are examined, it is seen that the convergence is tested based on public expenditures and tax revenues, which are among the fiscal policy instruments. When the relevant studies are examined, it is seen that most of them focus on EU countries and OECD countries. By Blanco et al. (2020), the existence of convergence in public R&D expenditures in EU countries could not be determined. Barrios et al. (2019) identified seven convergence clubs for the patents as a proxy for innovation activities among EU. While Angelov (2019) analysed the convergence of public spending on education services in EU countries, Halaskova et al. (2020) analysed the convergence of functional public expenditures in 7 EU countries. According to the findings, similar and different aspects have been revealed in the level of public expenditures in EU countries. Raleva (2020) analysed the convergence of Bulgaria to the EU, considering the shares of public expenditures in GDP, and concluded that the obtained findings contradict the real convergence. While a convergence was detected in the size of public expenditures in the relevant countries, no convergence could be detected between public expenditures and public expenditure components that can be considered efficient. This shows that each country implements different policies in EMU countries. In the studies conducted based on OECD countries, it is determined that there is a convergence in fiscal policies among OECD countries (Rompuy, 2021; Göğül and Korap, 2014), while some studies (Lichtenberg, 1994; Sanz and Velazquez, 2001; Sanz and Velazquez, 2004) concluded that there is no convergence. Akram and Rath (2019, 2022) reached the existence of convergence in terms of public revenues and public debt among regions in India and reveal that there is convergence in the case of the states being divided into three clubs in India. Mahdavi and Westerlund (2018) did not find the existence of convergence in tax revenues and tax effort in the 48 states of the USA. In line with the findings, it is revealed by emphasising the studies in the literature that there is fiscal diversity among the states of the USA and that this situation should continue. Clemente et al. (2019), on the other hand, concluded that there is no single pattern behavioural model in health expenditures in the USA and that there is a convergence of two different clubs. Chen et al. (2019) state that there was no convergence in environmental public expenditures in 30 provinces in China. Luintel et al. (2020), on the other hand, states that education and health expenditures contribute more to the convergence among provinces of China. Rahman et al. (2020), while detecting the existence of sigma convergence among tax revenues in the 2010–2017 period in 33 provinces of Indonesia, concluded that there is no absolute and conditional convergence. It is stated that there is a disparity in tax revenues due to the lack of fiscal convergence among provinces of India. Apergis and Cooray (2014) concluded that there is no convergence in tax revenues for 11 ASEAN countries, Asia Pacific, and Oceania countries. In Traore (2021), it was concluded that there is no convergence in public health expenditures in Sub-Saharan African countries, but there is convergence in eight clubs and divergence in one club according to club convergence test results.
From this point of view, study aims to investigate the existence of convergence in Turkiye in the period of 2004:01–2020:12, taking into account the fiscal aim based on incentive regions. Within the scope of this aim, the effectiveness of the fiscal policy implemented in Turkiye can be measured, and in line with the results, important implications will be achieved in terms of increasing the efficiency of the policies to be implemented. The study, which analyses the convergence of fiscal policies within the scope of incentive regions in Turkiye, aims to contribute to the literature at this point by identifying gaps in the literature. First, there are empirical studies examining the convergence of public expenditures and tax revenues across Turkiye (Sağbaş, 2002; Yamanoğlu, 2008; Allahverdi et al., 2021; Tekdere and Çadırcı, 2022). However, when these studies are examined, it can be seen that none of them examines interregional convergence within the scope of fiscal aim to close the budget deficit. Analysing only the convergence of public expenditures or tax revenues shows the one-way convergence of fiscal policy instruments. Still, it does not provide sufficient information on the main objective of states, which is to ensure budget balance. Therefore, this study fills this gap. Because as mentioned, the fact that public expenditures are higher than public revenues causes a budget deficit. For this reason, the findings from the study show which regions achieve more of the fiscal aim in Turkiye. Results at the end of the study may provide new insights into ensuring horizontal equality among the regions in Turkiye.
Secondly, in convergence analysis, it is thought that the use of the Evans–Karras test in the case of linearity and the Panel Threshold Unit Root Test (Panel TAR), which was developed by Beyaert and Camacho (2008), allows for absolute or conditional analysis of convergence as well as linearity and stationarity test, and will contribute to the literature.
The rest of the paper is organised as follows. Section 2 briefly describes the methodology. Section 3 reports empirical results from the Panel Threshold Unit Root Test (Panel TAR) tests, and conclusions and policy implications are summarised in the last section.
This section describes the dataset and empirical analysis method, including the Panel Threshold Unit Root Test (Panel TAR) and Evans–Karras linearity convergence test. The reason why Panel Threshold Unit Root Test (Panel TAR) and Evans–Karras linearity convergence test are used in convergence analysis is valid only if economies have identical first-order autoregressive dynamic structures and all permanent cross-economy differences are completely controlled for conditions that are grossly violated for the data sets considered here (Evans and Karras, 1996). At the same time, the rationale is based on the belief that the convergence process is not uniform in the following sense. In the first place, the countries may only converge if certain institutional, political, or economic conditions are fulfilled, whereas they may diverge otherwise. Another possibility is that convergence occurs at one rate in certain conditions and at another one under other conditions. Thus, Panel Threshold Unit Root Test (Panel TAR) and Evans–Karras linearity convergence test provide the unit root test and other assumptions (Beyaert and Camacho, 2008). For this reason, tests have robustness estimators.
Barro and Sala-i Martin (1992) used the β convergence regression in their study, which is cited as the pioneering work on convergence analysis, and then this convergence method was criticized on the grounds that it did not give consistent results because it was estimated by linear regression method and the series used were not stationary. Because, the series used in convergence analysis must be free from the unit root. From this point of view, the opinion that estimation by nonlinear methods will be consistent and error-free in interpreting the obtained results has gained validity (Beyaert and Camacho, 2008). In this context, the Threshold Autoregressive (TAR) Panel Unit Root test was developed by Beyaert and Camacho (2008). The development of the test was based on the study by Evans and Karras (1996). Accordingly, Evans and Karras first used the following model to test the existence of real convergence with panel data in a linear framework where the convergence rate of a particular country is assumed to be constant (Evans and Karras, 1996):
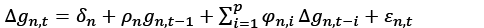 (1)
(1)
In the equation n=1, …, N and T=1, …. ,. n represent the cross-section units, and t represents the period, representing the cross-sectional units’ per capita income. In the equation, if ρn=0, it indicates divergence; if 0<ρn<1, it indicates convergence. Here, it is mentioned that absolute convergence exists if ρn=0 and conditional convergence exists otherwise (Evans and Karras, 1996).
The procedure of the convergence test developed by Evans and Karras (1996) is as follows: In the first step, ordinary least squares (OLS) are applied to equation 1 to obtain the standard error of the estimation. Then, for each n, the normalised series 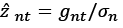 is calculated. In the second step, by applying the OLS estimate of ρ and the OLS to equation 2, the t ratio is obtained.
is calculated. In the second step, by applying the OLS estimate of ρ and the OLS to equation 2, the t ratio is obtained.
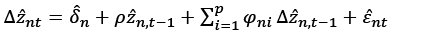 (2)
(2)
In the third step, if 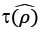 is greater than the appropriately chosen critical value, the hypothesis H0:∀n ρn = 0 is rejected in favour of the hypothesis H1:∀n ρn < 0. Otherwise, the H0 hypothesis is accepted. If H0 is rejected, the F-ratio is calculated in the final step.
is greater than the appropriately chosen critical value, the hypothesis H0:∀n ρn = 0 is rejected in favour of the hypothesis H1:∀n ρn < 0. Otherwise, the H0 hypothesis is accepted. If H0 is rejected, the F-ratio is calculated in the final step.
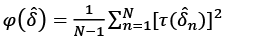 (3)
(3)
In the equation, 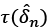 is the t-ratios of the δn estimator obtained by applying ordinary least squares to equation 1 for economy n. If
is the t-ratios of the δn estimator obtained by applying ordinary least squares to equation 1 for economy n. If 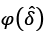 is greater than the appropriately chosen critical value, it represents conditional convergence, and if it is small, it represents absolute convergence.
is greater than the appropriately chosen critical value, it represents conditional convergence, and if it is small, it represents absolute convergence.
However, the above equation assumes that the convergence process will be uniform. Convergence is a situation that produces different results depending on certain conditions (Beyaert and Camacho, 2008). For this reason, a new generation unit root test was developed by Beyaert and Camacho (2008), which considers the dependency and linearity between the horizontal sections that make up the panel. This test considers three main approaches: (1) determining a threshold value for the panel, (2) performing unit root tests for both regimes and all, and (3) testing all results with the bootstrap method. Beyaert and Camacho rearranged equation (1), developed by Evans and Karras to test convergence with panel data, as equation (2), assuming that convergence is not uniform (Beyaert and Camacho, 2008).
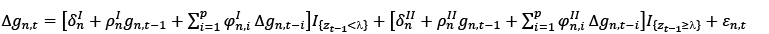 (4)
(4)
In equation (4), I {x} is an indicator that takes the value 1 when x is true and 0 otherwise. Therefore, if the condition 𝑧𝑡−1 < 𝜆 is met, the variable that takes a unit value acts as a dummy variable. If 𝑧𝑡−1 < 𝜆 and “regime II”, then the situation with 𝑧𝑡−1 ≥ 𝜆 is called “regime I”. Therefore, 𝜆 is a “threshold” parameter, and equation (2) belongs to the class of threshold autoregressive (TAR) models primarily developed by Tong (1978).
When equation (4) is estimated, its superiority needs to be checked against the linear Evans–Karras model (1). If confirmed, the next step consists of testing for convergence by applying some unit root test to the 𝜌 coefficients of equation (4). Finally, if there is evidence of convergence, the final step is to test the 𝛿 coefficients of equation (2) with a final test against conditional convergence.
In a one-equation TAR framework, critical values are obtained by bootstrapping simulations by Hansen (1996) and Caner and Hansen (2001). In the next stage, the following hypothesis is tested (Beyaert and Camacho, 2008).
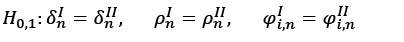 (5)
(5)
Since all coefficients are not equal in both regimes when ∀n=1,…, N, and ∀i=1,…,p in the hypotheses, equation (1) is estimated by FGLS method, and equation (4) is estimated by the grid-FGSL one. For each model, the value of the likelihood function at the prediction point is calculated, and the value £12=-2ln(L1/L2) is obtained. L1 is the single regime linear model equation for equation (1), and L2 is the realisation value of the two-regime TAR model. If £12 is too big, the H0 hypothesis indicating linearity is rejected. Critical values about how much this size should be are also obtained from the studies of Caner and Hansen (2001). As a result of the boot method, since the unit root detection is not done yet, two models are obtained as “restricted” and “unrestricted”. The linearity of both models is tested. If both models are not linear simultaneously, the panel TAR method can be applied (continuing from equation (4)). If one or both of the models are linear, the panel TAR method cannot be applied (continuing from equation (1)) (Eryüzlü and Hopoğlu, 2020). Continuing from equation (2), the H0,2 hypothesis is as follows:
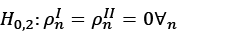 (6)
(6)
The validity of equation (4) shows that two different regimes are valid for the country. While the threshold value of these regimes is revealed, regime one shows the times when the data in question is above the threshold value, and regime two shows the opposite situation. As noted above, the test considers three main approaches: setting a threshold for the panel, separate unit root tests for both parts (regimes), and all. These three situations are tested as follows (Beyaert and Camacho, 2008).
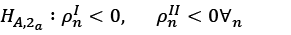 (7)
(7)
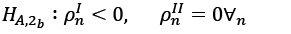 (8)
(8)
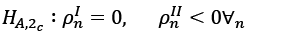 (9)
(9)
Hypothesis (2a) reflects the convergence of sections under regimes one and two. This situation is called “full convergence”. Other hypotheses (2b) and (2c) imply that convergence occurs only under regime one or only under regime two. Such a situation is called “partial convergence”.
A few test statistics from the work of Caner and Hansen (2001) are used to distinguish the three main approaches. The test statistics suggested by Caner and Hansen are given in equation (10) (Caner and Hansen, 2001).
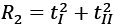 (10)
(10)
Here X is the grid-FGLS estimate of Y in model 1 for i = 1, and Y. Large R2 values are favourable for convergence. On the other hand, if the hypothesis of convergence under the 1st regime (equation (4)) and differentiation under the 2nd regime (equation (1)) cannot be rejected in the case where t1 is very small and t2 is absent, to find the appropriate probability values, bootstrapping is critical. (Yavuz and Yılancı, 2013).
The final step of convergence analysis consists of distinguishing between absolute and conditional convergence. The hypotheses proposed are as follows:
 (11)
(11)
 (12)
(12)
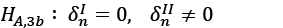 (13)
(13)
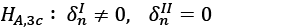 (14)
(14)
Under the main hypothesis, 𝜌in < 0, ∀𝑛, 𝐻0,3 indicates absolute convergence under both regimes and the alternative in 𝐻𝐴,3𝑎 affects conditional convergence. Alternative hypotheses 𝐻𝐴,3𝑏 and 𝐻𝐴,3𝑐 imply conditional convergence in the first and second regimes and absolute convergence in the second and first regimes, respectively. The null hypothesis is tested using the ∅𝑗,𝑗 = 𝑎, 𝑏, 𝑐 tests of Beyaert and Camacho (2008). Critical values are obtained by bootstrapping simulations (Yavuz and Yılancı, 2013).
Public expenditures and tax revenues were obtained from the database of the Ministry of Treasury and Finance, General Directorate of Public Accounts. The most basic indicator used in calculating the fiscal aim of taxes is tax revenues/public expenditures. For this reason, the ratio of tax revenues to public expenditures is considered in the analysis.
Budget deficits, which hurt the overall macroeconomic performance of the country, are among the most important problems in Turkiye, as in most countries (Özsoy, 2008). As mentioned above, among the main causes of budget deficits are the higher increase in public expenditures compared to public revenues and the more significant fluctuation in tax revenues over the years. In other words, in Turkiye, tax revenues cannot adequately meet the fiscal aim. This situation in Turkiye can be seen in Figure 1.
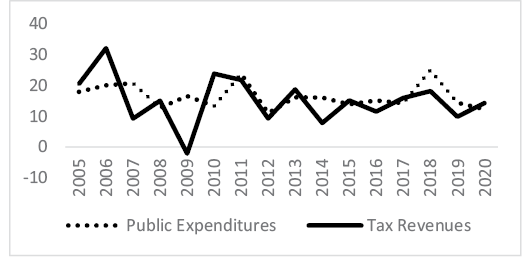
Figure 1 shows the growth rates of public expenditures and tax revenues in Turkiye over the years. Accordingly, growth rate of tax revenues has fluctuated over the years, and there have been sharp declines in general. On the other hand, the growth rate in public expenditures has been following a more stable course over the years. This may cause budget deficits. Although there are budget deficits in Turkiye, regional development policies have been implemented, especially since the 1960s. With the development policies implemented in Turkiye, balanced income distribution among regions and classes has been determined as the main target, and state-led plans have begun eliminating regional disparities (Dökmen and Tekbaş, 2011). Within the scope of this policy, Turkiye is divided into six regions, taking into account the socio-economic development of the provinces. Accordingly, regional incentive practices based on the fiscal instruments applied in each region differ. In regions with less socio-economically developed provinces, more public expenditures are realised. At the same time, fewer tax revenues are collected in line with basic objectives such as improving investments and income distribution. On the other hand, the opposite situation occurs in regions with socio-economically developed provinces. This causes differences among regions in terms of meeting the fiscal aim of taxes. This situation in Turkiye makes the convergence of fiscal policies across the country even more important. The convergence in fiscal policies among regions indicates that the fiscal aim realises the policies implemented. In contrast, the absence of convergence indicates that the resources are not used in productive areas.
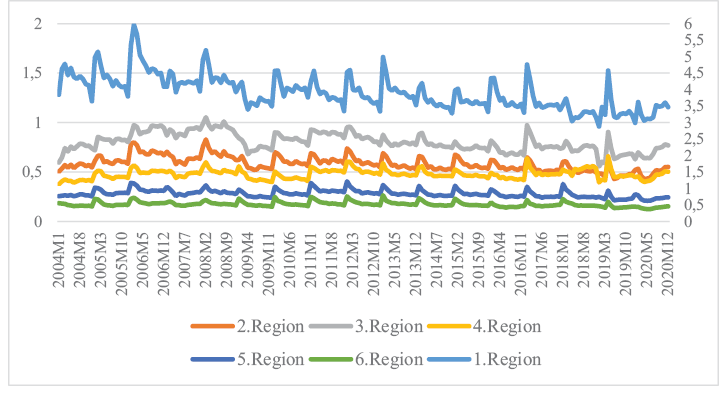
In Figure 2, the first region is shown on the secondary axis, and the other regions are shown on the primary axis. Accordingly, it is seen that the first region contributes the highest part to closing Turkiye’s budget deficit. Apart from the first region, it is seen that the other regions are quite close to each other. Table 1 contains the descriptive statistical information of the data used in the analysis.
|
Regions |
Obs. |
Mean |
St. Dev. |
Min. |
Max. |
|
1. Region |
204 |
3.909 |
0.527 |
2.881 |
5.971 |
|
2. Region |
204 |
0.584 |
0.075 |
0.429 |
0.829 |
|
3. Region |
204 |
0.802 |
0.096 |
0.555 |
1.054 |
|
4. Region |
204 |
0.478 |
0.048 |
0.375 |
0.658 |
|
5. Region |
204 |
0.281 |
0.038 |
0.209 |
0.405 |
|
6. Region |
204 |
0.173 |
0.025 |
0.124 |
0.265 |
As seen in Table 1, tax revenues in the first region are considerably higher than public expenditures (3.909%). On the other hand, the third region is in second place regarding taxes serving a fiscal aim. Looking at other regions, it is seen that tax revenues are realised below public expenditures. In other words, taxes in other regions, except the first region, do not meet the fiscal aim. The sixth region is in the last place in meeting the fiscal aim. This region has the least developed provinces in terms of socio-economics. This situation shows that the burden of closing the budget deficits in Turkiye is mainly concentrated in the first region.
In the study, convergence in the fiscal policy applied based on the fiscal aim of taxes in Turkiye by region was analysed with the help of the panel data method. In this context, the panel threshold unit root test developed by Evans and Karras (1996) and Beyaert and Camacho (2008) was used. The analysis consists of four stages. In the first stage, the threshold value is determined for the data used in the study. In the second stage, the linearity of the data is tested, and if the linearity result is reached, the Evans and Karras (1996) procedure is applied. The Beyaert and Camacho (2008) procedure is applied if the nonlinearity result is achieved. In the third stage, the existence of convergence between regions is tested. In the fourth and final stage, the type of convergence is determined. The results of the convergence analysis are given in Table 2.
|
Linearity tests |
Transition Region |
d |
λ |
% observation in regime 1 |
|
|
Unrestricted |
Restricted |
||||
|
1.000 |
1.000 |
2 |
12 |
0.57 |
15.26 |
According to the results in Table 2, it was concluded that the H0 hypothesis was linear because the H0 hypothesis could not be rejected according to the constrained and unconstrained model. Therefore, the analysis should continue with the procedure proposed by Evans and Karras (1996). Table 3 shows the analysis results of Evans and Karras (1996).
|
Divergence versus convergence |
Absolute versus conditional convergence |
|
|
Bootstrap p-value |
0.010 |
0.261 |
|
Result |
Convergence |
Absolute convergence |
According to the results of the Evans-Karras (1996) model in Table 3, it is concluded that there is a strong convergence in the interregional fiscal policy in Turkiye because the convergence versus divergence hypothesis is rejected. When we look at the type of convergence, since the H0 hypothesis cannot be rejected, it is mentioned that there is absolute convergence. The fact that the policies implemented have the same steady-state development rate in the fiscal policies of the regions, in the long run, proves the validity of absolute convergence. As seen in Figure 2, all regions are linear by periods. In other words, the Keynesian fiscal theory is supported in the fiscal policy implemented by regions in Turkiye. In other words, the fiscal policy implemented in Turkiye can be interpreted as reaching the expected aims of eliminating regional disparities and convergence of regions. According to the findings, there is a convergence in the fiscal policy implementation between regions in Turkiye. The existence of convergence is similar to the studies in the literature (Akram and Rath (2022), Rahman et al. (2020), Göğül and Korap (2014), and Rompuy (2021)). The findings are similar to Rahman et al. (2020). Indeed, Rahman et al. (2020) concluded that there is a disparity among provinces in implementing fiscal policies. The findings obtained by us also show that there is a disparity in fiscal aim among regions of Turkiye. Findings also reported by Allahverdi et al. (2021) confirm the conclusion that the average expenditure is low in the cluster where the most developed provinces of Turkiye are located. As a matter of fact, in the first region, where the most developed provinces are located, public expenditures were lower than tax revenues. The findings, again obtained by Traore (2021), show that all groups converge and one group differs and supports each other.
In table 1, it is seen that the ratio of tax revenues to public expenditures in regions except the first region is below one and very close to each other. Among these five regions, the sixth region has the lowest value. The main reason for separating the first and third regions from the other four regions is the socio-economic separation of these two regions from the other regions.
The ratio of tax revenues to public expenditures in the first region is above one, and it is seen that the tax revenues obtained in the region are more than the expenditures received from the region. This result can be explained in two ways: the concentration of resource allocation in the country in the first region, the tax structure, and the effect of the taxation procedure.
The first region in Turkiye is positively differentiated from other regions due to technological, geopolitical, production style, saving tendency, and industrialisation. As a natural consequence of this, it is determinative that tax revenues are higher than the public expenditures of the region. This situation causes an increase in migration from other regions to the first region in Turkiye. As a matter of fact, Istanbul, the most important province of the first region, has the highest population density in Turkiye. This situation causes some disruptions in the provision of public services in the first region. At the same time, investments are shifting from other regions to the first region. Because the first region is more developed in terms of infrastructure and supply chain, the government has initiated a general and regional incentive system to eliminate regional disparities. Under this system, less developed regions are given more privileges. Thus, it is aimed to stop the increasing migration from less developed regions and even initiate reverse migration.
The shift of the tax structure in Turkiye to indirect taxation, which has been embodied in Value Added Taxes and Special Consumption Taxes in recent years, is determinant in the separation of the first region. The concentration of the country’s population and trade in the first region causes the indirect tax base to shift to this region. As a result, it causes the taxes collected from the region to exceed the public expenditures of the region.
The fact that the taxation procedure is operated through the companies’ headquarters is another factor that distinguishes the first region from other regions. Although the companies carry out their production activities in other regions, they prefer to keep their headquarters in the first region. As a result, the financial centres of the companies are concentrated in this region. As a matter of fact, according to the Corporate Tax Law in Turkiye, the taxation of the branches is carried out through the administrative centres. This, while benefiting from public expenditures in the places where the units of large firms operate, causes the ratio of taxes to meet public expenditures to remain low in the regions where they operate because taxes are paid by their headquarters.
Public expenditures and tax revenues, which are among the fiscal policy instruments, are among the most important instruments used by the states. With these instruments, governments can effectively distribute resources and income among regions in the country. However, the increase in the disparity between public expenditures and tax revenues may expose the country to budget deficits. For this reason, the fiscal aim should be considered in using these instruments. The study reveals the existence of convergence among regions in terms of fiscal aim in Turkiye. According to the findings, there is a strong absolute convergence in the interregional fiscal policy in Turkiye. It is seen that the ratio of tax revenues to public expenditures in the 2nd–6th regions is below one and very close to each other. But in the first region, this ratio is above one. The first region of Turkiye is positively differentiated from other regions due to technological, geopolitical, production style, saving tendency, and industrialisation. As a natural consequence of this, it is determinative that tax revenues are higher than the public expenditures of the region. Although it is mentioned that there is an absolute convergence in regions other than the first region, it can still be stated that there is a significant disparity between the first region and the other regions. Although the state has implemented general and regional incentive policies to overcome this situation, it is seen that its aim has yet to be fully achieved.
Based on the results, to increase the fiscal convergence between the first region and other regions:
1) taxation in terms of administration is carried out in the region where the economic activity is carried out;
2) in the context of fiscal policies, a selective resource allocation policy should be followed to ensure the redistribution of resources concentrated in the first region, considering each region’s comparative advantage.
Finally, to discuss unity in any country, it is important to eliminate disparities among the regions and bring them to similar levels and implement the policies to be followed in this regard. For this, it is necessary to ensure convergence in the fiscal policies implemented within the country. In Turkiye, this should be one of the primary policy aims for policymakers.
Akram, V., Rath, B.N. (2019). Does debt convergence hold in case of India? Journal of Economic Studies, Vol. 46, issue 4, p. 858–871. https://doi.org/10.1108/JES-02-2018-0064
Akram, V., Rath, B. N. (2022). Does government revenue converge across Indian states? Evidence from club convergence. Applied Economics Letters, Vol. 29, issue 10, p. 915–919. https://doi.org/10.1080/13504851.2021.1897734
Allahverdi, Z. F., Allahverdi, M., Çevik, S. (2021). Türkiye’de kamu harcamalarının il düzeyinde dağılımının çok boyutlu ölçekleme ve kümeleme analizi ile incelenmesi. Maliye Dergisi, Vol. 180, p. 31–60. Retrieved from https://ms.hmb.gov.tr/uploads/2021/07/02-180-8-Tu%CC%88rkiyede-Kamu-Harcamalarinin-I%CC%87l-Du%CC%88zeyinde-Dag%CC%86ilimi.pdf
Angelov, A.G. (2019). Public Expenditure on Education in the EU Member States: A Cluster Analysis. Economic Archive, Vol. 72, issue 1, p.52–64.
Apergis, N. (2015). Convergence in public expenditure across a sample of emerging countries: evidence from club convergence. Emerging Markets Finance & Trade, Vol. 51, issue 3, p.448–462. http://doi.org/10.1080/1540496X.2015.1025670.
Apergis, N., Cooray, A. (2014). Tax revenues convergence across ASEAN, Pacific and Oceania countries: Evidence from club convergence. Journal of Multinational Financial Management, issue 27, p.11–21. http://dx.doi.org/10.1016/j.mulfin.2014.06.007.
Barrios, C., Flores, E., Martinez, M. A. (2019). Club convergence in innovation activity across European regions. Papers in Regional Science, Vol. 98, issue 4, p.1545–1565. http://dx.doi.org/10.1111/pirs.12429.
Beyaert, A., Camacho, M. (2008). TAR Panel Unit Root Tests and Real Convergence. Review of Development Economics, Vol. 12, issue 3, p.668–681. https://doi.org/10.1111/j.1467-9361.2008.00479.x
Blanco, F. A., Delgado, F. J., Presno, M. J. (2020). R&D expenditure in the EU: convergence or divergence?. Economic Research-Ekonomska Istraživanja, Vol. 33, issue 1, p.1685–1710. https://doi.org/10.1080/1331677X.2020.1756371
Caner, M., Hansen, B. (2001). Threshold Autoregression with a Unit Root. Econometrica, issue 69, p. 1555–1596. Retrieved from https://www.jstor.org/stable/2692267#metadata_info_tab_contents
Chen, S., Song, Y., Ding, Y, Qian, X., Zhang, M. (2019). Research on the strategic interaction and convergence of China’s environmental public expenditure from the perspective of inequality. Resources, Conservation & Recycling, Vol. 145, p. 19–30. https://doi.org/10.1016/j.resconrec.2019.02.017
Clemente, J., Lazaro-Alquezar, A., Montanes, A. (2019). US state health expenditure convergence: A revisited analysis. Economic Modelling, Vol. 83, p. 210–220. https://doi.org/10.1016/j.econmod.2019.02.011.
Dökmen, G., Tekbaş, A. (2011). Türkiye’de kamu harcamalari ve kamu gelirlerinin bölgesel analizi. İstanbul Üniversitesi İktisat Fakültesi Maliye Araştırma Merkezi Konferansları, issue 56, p. 95–120. Retrieved from https://dergipark.org.tr/en/download/article-file/455822.
Eryüzlü, H., Hopoğlu, S. (2020). Devlet Politikalarının Şirket Açılış ve Kapanışı Üzerindeki Etkileri: Türkiye İçin Ekonometrik Bir Analiz, 2010-2018. Journal of Social Sciences of Mus Alparslan University, Vol. 8, issue 1, p. 297–303. Retrieved from https://dergipark.org.tr/tr/download/article-file/973336.
Evans, P., Karras, G. (1996). Convergence Revisited. Journal of Monetary Economics, Vol. 37, issue 2, p. 249–65. https://doi.org/10.1016/S0304-3932(96)90036-7
Göğül, P. K., Korap, L. (2014). Ekonomik yakınsama olgusunun sınanması üzerine yeni bulgular: OECD örneği. Kastamonu Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi, issue 4, p.60–73. Retrieved from https://dergipark.org.tr/tr/download/article-file/303224
Halaskova, M., Halaskova, R., Bednar, P. (2020). Public Services and their Financial Allocation in the European Context. Scientific Papers of the University of Pardubice, Series D: Faculty of Economics and Administration, Vol. 28, issue 2, p. 1–9.
Hansen, B. E. (1996). Inference when a nuisance parameter is not identified under the null hypothesis. Econometrica: Journal of the econometric society, Vol. 2, issue 64, p. 413–430.
Lichtenberg, F. R. (1994). Testing the convergence hypothesis. The Review of Economics and Statistics, Vol. 76, issue 3, p. 576–579, Retrieved from https://www.jstor.org/stable/2109982#metadata_info_tab_contents.
Luintel, K. B., Matthews, K., Minford, L., Valentinyi, A., Wang, B. (2020). The role of Provincial Government Spending Composition in growth and convergence in China. Economic Modelling, Vol. 90, p. 117–134. https://doi.org/10.1016/j.econmod.2020.04.024.
Mahdavi, S., Westerlund, J. (2018). Subnational Government Tax Revenue Capacity and Effort Convergence: New Evidence from Sequential Unit Root Tests. Economic Modelling, Vol. 73, p. 174–183. doi:10.1016/j. econmod.2018.03.016.
MTF (2022). General Government’s Financial Statistics. Republic of Turkiye, Ministry of Treasury and Finance. https://muhasebat.hmb.gov.tr/genel-butce-gelirlerinin-iller-itibariyle-tahakkuk-ve-tahsilati-2004-2019
Özsoy, O. (2008). Government budget deficits, defence expenditure and income distribution: the case of Turkiye. Defence and Peace Economics, Vol. 19, issue 1, p. 61–75. https://doi.org/10.1080/10242690701347689.
Rahman, Y. A., Oktavilia, S., Fafurida, Karsinah. (2020). Tax Revenue Convergence Among Provinces in Indonesia. Advances in Natural and Applied Sciences, Vol. 14, issue 2, p. 198–204.
Raleva, S. (2020). Bulgarian gdp expenditure structure: growth impact and convergence with Eurozone. Yearbook of Unwe, issue 1, p. 167–191.
Rompuy, P. V. (2021). Does subnational tax autonomy promote regional convergence? Evidence from OECD countries, 1995–2011. Regional Studies, Vol. 55, issue 2, p. 234–244. https://doi.org/10.1080/00343404.2020.1800623
Sağbaş, İ. (2002). Türkiye’de kamu harcamalarının yakınsama üzerindeki etkisi. Afyonkocatepe Üniversitesi İİBF Dergisi, Vol. 4, issue 2, p. 137–148. Retrieved from https://dergipark.org.tr/tr/download/article-file/19099
Sanz, I., Velázquez, F. J. (2001). The evolution and convergence of the government expenditure composition in the OECD countries: an analysis of the functional distribution. (Working Paper, No: 9/2001), European Economy Group. Retrieved from https://www.researchgate.net/publication/23749022
Sanz, I., Velázquez, F. J. (2004). The Evolution and Convergence of the Government Expenditure Composition in the OECD Countries. Public Choice, Vol. 119, issue 1/2, p. 61–72. Retrieved from http://www.jstor.org/stable/30025813
Smith, A. (1977). An Inquiry Into the Nature and Causes of the Wealth of Nations – England, Cambridge University Press.
Tanzi, V. (2005). Fiscal policy and fiscal rules in the European union. (Studies & Analyses No. 301). Center for Social and Economic Research. Retrieved from https://ssrn.com/abstract=1441917.
Tekdere, M., Çadırcı, B. D. (2022). Türkiye’de il düzeyindeki mahalli idare harcamalarının yakınsama analizi. Sosyoekonomi, Vol. 30, issue 52, p. 379–407. Retrieved from https://dergipark.org.tr/tr/download/article-file/1904172.
Terra, F. H. B., Filho, F. F., Fonseca, P. C. D. (2021). Keynes on State and Economic Development. Review of Political Economy, Vol. 33, issue 1, p. 88–102. https://doi.org/10.1080/09538259.2020.1823072
Tevdovski, D., Jolakoski, P., Stojkoski, V. (2021). Determinants of budget deficits: Focus on the effects from the COVID-19 crisis. (MPRA Paper 108056), University Library of Munich, Germany. https://doi.org/10.48550/arXiv.2105.14959
Tokatlıoğlu, M., Selen, U. (2019). Maliye Politikası (Second edition) - Bursa, Ekin Basım Yayın.
Tong, H. (1978). On a Threshold Model. in C. Chen (ed.), Pattern Recognition and Signal Processing, Amsterdam: Sijhoff and Noordhoff.
Traore, O. (2021). Convergence in public health expenditure across the Sub-Saharan African countries: does club convergence matter?. Health Econ Rev, Vol. 11, issue 21, p. 1–14. https://doi.org/10.1186/s13561-021-00316-0
Winner, H. (2005). Has Tax Competition Emerged in OECD Countries? Evidence from Panel Data. International Tax and Public Finance, Vol. 12, p. 667–687. https://doi.org/10.1007/s10797-005-2915-0
Yamanoğlu, K. B. (2008). Türkiye’de sosyo-ekonomik faktörlerin iller arasi yakinsama üzerine etkileri. İstatistikçiler Dergisi, Vol. 1, p. 33–49. Retrieved from https://dergipark.org.tr/tr/download/article-file/105636
Yavuz, N. Ç., Yılancı, V. (2013). Convergence in Per Capita Carbon Dioxide Emissions Among G7 Countries: A TAR Panel Unit Root Approach. Environ Resource Econ, Vol. 54, p.283–291. https://doi.org/10.1007/s10640-012-9595-x