Ekonomika ISSN 1392-1258 eISSN 2424-6166
2019, vol. 98(1), pp. 60–80 DOI: https://doi.org/10.15388/Ekon.2019.1.4
Evaluating the State of Health Care Institutions: The Case of Lithuanian Municipalities
Vaida Breimerytė, Vytautas Kėdaitis, Algirdas Miškinis,* Kęstutis Trainavičius
Vilnius University, Lithuania
Abstract. Huge differences between the territories that are divided into the city and district municipalities are found after examining theoretical and methodological literature, obtaining abundant statistical information on the status of health care institutions in Lithuania, disclosing the system of indicators describing that status, and taking into account the analysis of the data of all the statistic residents of the Territorial Health Insurance Funds (THIF) and those registered at the outpatient primary personal health care institutions (OPPHCI). The number of residents who have registered at the OPPHCI of city municipalities is different from the rates provided by the statistics. Therefore, in the calculation of health indicators, a meaningful selection of them will more accurately reflect the status of health care facilities. Of these indicators, it is important to select not only those that best describe the existing medical care level in the municipalities but those that are also informative. The system of indicators was selected on the basis of the Delphi method. This article analyzes the state of the health care institutions in Lithuania and the qualitative and quantitative indicators of health care and their evaluation at the municipal level. The authors of this article used multivariate statistical methods in evaluating the state of health care institutions. The reliability and the validity of the obtained results are verified by two models; thus, the stability and suitability of the models are tested in investigating the state of health care institutions in Lithuania. The final aim of the study is to evaluate the administrative units of different territories and, from the medical level perspective, identify the best performing and most lagging municipalities.
Keywords: health care institutions, composite indicator, factor analysis, principal component analysis.
* Corresponding author:
Department of Economic Policy, Faculty of Economics and Business Administration,
Vilnius University, 9 Saulėtekio Ave., LT-10222, Lithuania
Email: algirdas.miskinis@evaf.vu.lt
Received: July 2018. Revised: October 2018. Accepted: November 2018
Copyright © 2019 Vaida Breimerytė, Vytautas Kėdaitis, Algirdas Miškinis, Kęstutis Trainavičius. Published by Vilnius University Press
This is an Open Access article distributed under the terms of the Creative Commons Attribution Licence, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
1. Introduction
In a contemporary society, health is referred to as a value, the preservation of which is a goal in the process of an increasingly growing emphasis on improving the efficiency of health care. According to the World Health Organization, health is “one of the key rights of every human, regardless of race, religion, political beliefs, economic or social status,” and each government must facilitate the access to health care for each individual.
In most countries, the largest part of health care expenditure is covered by the public sector. Although each country has its own health care system that can not be automatically accepted or adapted by others due to various economic, social, or financial differences, all the countries seek to ensure a better quality of health care services through the increase in the efficiency of the national health system, a rational allocation of resources, the provision of health care accessibility to all social groups, and the promotion of disease prevention. Therefore, it is important for each country to create a sustainable mechanism for managing its health care system, saving on budgetary funds, and improving human health (Leiyu Shi 2012).
An important role in the health care system is played not only by the political institutions but also by the general public and the medical institutions as the direct providers of health care, which are sometimes deprived of their primary role. The coordination of patient health care by personal health care providers can be termed as a public good that benefits not only the individual but the general society as well. Unfortunately, institutions are sometimes burdened by a large number of regulatory acts, the increased workload of physicians and other bureaucratic features that directly affect the relationship between doctors and patients.
The scientific problem this article deals with: health care is a continuous process that requires permanent research, improvement and, most importantly, a source of ongoing funding. Health care costs are continuously rising not only in Lithuania but worldwide as well (Čepulytė, Palubinskienė 2008; Čiburienė 2012). In the future, due to the changing structure of the global population, a further increase in health care costs is anticipated. An intensive growth in the elderly population and an increase in the average life expectancy will pose the need for health care services and for nursing in particular. A decrease in the population is being recorded in Lithuania; this problem is prone to grow even more, driven by the rising numbers of emigration, and can become an unbearable burden on the state and its society. Due to emigration, an accelerating loss in doctors, as well as their uneven geographical distribution, is observed in Lithuania.
The aim of the study is to analyze health indicators in different municipalities using multivariate models and to rank municipalities according to their level of health care services provision.
Research methods – factor analysis and principal component analysis, calculation of the composite indicator of municipalities.
2. Statistical Models for the Evaluation of Health Care Institutions
This study evaluated personal health care institutions in Lithuanian municipalities. Grouping based on only a few indicators or the use of traditional statistical methods would have been inappropriate, since the actual picture would not be seen. Therefore, several methods were used in this study, i.e., the principal components and factor analysis methods, which helped to clarify and describe the relationship between the health indicators under analysis. Also, the calculation of a composite indicator of municipalities helped to rank these health care institutions according to the level of medical services.
1. The scientific literature describes the principal component analysis method as a method for reducing data dimensions, in which several principal components cover a substantial part of data dispersion (Porcelli 2009; Husson 2010).
2. The aim of the factor analysis is to divide the indicators under analysis into certain factors that are linked by a correlation with the minimal loss of the amount of information (McKillop et al. 2012; Tanna 2009). A shift from variables to factors allows researchers to summarize information, which is made more understandable and easier to interpret.
The main difference between these methods is that the principal component analysis is applied to reduce the amount of data and is oriented toward dispersion, while the factor analysis is used to explain the correlation between the initial variables. The use of multivariate models enables the distribution of municipalities by factors/components. To perform a comparative analysis of municipalities with different features, a methodology of the composite indicator will be used in this study.
2.1. Factor Analysis, Its Use and Purpose
At the beginning of the study, the analysis of large quantities of different indicators – medical, economic, social, and other indicators, for example – may prove it difficult to determine which of these indicators are essential. Factor analysis (Kėdaitis 2001) was used to solve this problem.
The main idea of factor analysis is that the observed variables are grouped according to their intercorrelations. We assume that the variables of each group are determined by some non-observable (latent) factor. The researchers select this factor by themselves when examining the variables that make up the groups. Factor analysis then allows the researchers to manipulate a large amount of data when there are many indicators, and this is done to determine the number of non-observable factors and to evaluate the clarification of factors by data and data interpretation. However, factor analysis may not be appropriate in all cases, as not all the factors will actually exist. The factors that are obtained do not always escape ambiguity, or the factors obtained cannot be easily interpreted. Therefore, researchers may pose questions regarding the extent of the reliability and objectivity of this method.
There are two types of factor analysis: exploratory and confirmatory. Taking into account the fact that the information on the number of factors to be obtained or which indicators would form groups in our study was not known before carrying out the research, exploratory factor analysis was used. Confirmatory factor analysis is used when factors are preliminarily outlined in advance.
Below is a mathematical model of factor analysis. Let us assume we have k of variables X1, X2, … , Xk. This model is based on the assumption that the behavior of each variable Xi is caused by m of the common latent factors F1, F2, … , Fm. There are fewer common factors than the variables. We let the variables Xi depend linearly on the factors. The task of the factor analysis is to determine, define the common factors Fi when we know only the values of Xi (Čekanavičius, Murauskas 2004).
The expression of the mathematical model is as foll
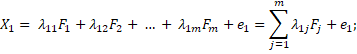
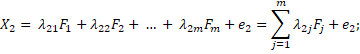
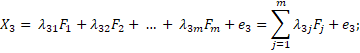
..............................................................................................
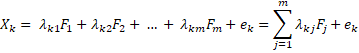 (1)
(1)
ei – specific (characteristic) latent factor, λij – factor weights
The weights of factors that are significantly different from 0 are important in carrying out factor analysis. According to R. Eidukavičius (1998), common factors are those that have at least two weights and are significantly different from zero. The factors with all weights significantly different from 0 are called generic. The factors that have 1 weight, significantly different from 0, are referred to as unitary or characteristic factors e1,…, e5).
The factor analysis assumptions are made as follows:
• the observed variables are distributed according to the normal distribution
Xi ~ N(μi,σi2 );
• common factors Fj are uncorrelated and DFj=1;
• characteristic factors ei are uncorrelated and Dei = τi;
• factors Fj and ei are uncorrelated, where i = 1, …, k, j = 1, …, m.
Taking into account these assumptions, the dispersions and covariations of the observed variables can be written as follows (Čekanavičius, Murauskas 2004):
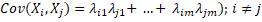 (2)
(2)
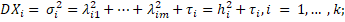 (3)
(3)
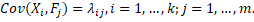 (4)
(4)
The sum of the squares of the common factors’ weights of the dimension hi2 (mathematically 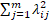 ) accounts for a common dispersion for the variable Xi; the next dimension τi is called specificity (a specific dispersion characteristic to that variable and not related to common factors).
) accounts for a common dispersion for the variable Xi; the next dimension τi is called specificity (a specific dispersion characteristic to that variable and not related to common factors).
2.2. Principal Component Analysis
Principal component analysis (PCA) is a linear data transformation widely used for data analysis as a method for reducing the number of dimensions of multivariate data (Kėdaitis 1999). This multivariate statistic method is most commonly used for a large number of indicators describing the phenomenon and a limited number of observations. According to G. Dzemyda, O. Kurasova, and J. Žilinskas (2008), the main idea of the model is “to reduce the number of data dimensions in processing the linear transformation and to abandon some of the new components with the lowest dispersion, obtained after transformation”. It can be argued that if several principal components cover the essential part of the data dispersion, then, instead of all the variables, only a few primary components can be used for studies.
The principal components are linear derivatives of the original variables and can be expressed as follows:
F1* = w11x1 + w12 x2 + · · · + w1p xp;
F2* = w21x1 + w22 x2 + · · · + w2p xp;
……………………………………
Fp* = wp1x1 + wp2 x2 + · · · + wpp xp; (5)
where: F1* , F2* , ..., Fp* – principal components, wij – weight (coefficient) of the j variable for the i principal component, xj – j primary variable
Weights wij are selected in line with the following circumstances:
1. The scale of the new variables must be fixed, as the change in the scale of the weights can increase the dispersion of linear structures: wi12 + wi22+ ... + wip2 = 1, i = 1, …, p.
2. The perpendicularity of new axes: wi1wj1 + wi2wj2 + ... + wipwjp= 0, in all i ≠ j.
3. Composite Indicator of Municipalities
The composite indicator will be used to rank municipalities according to their health care indicators (Vaškevičiūtė, Kėdaitis 2007). This indicator will be deployed to find one composite characteristic. The formula for the composite indicator will be derived using the vector-distance formula and the Pythagorean Theorem. The formula output will be provided according to municipality marked B in Fig. 1.
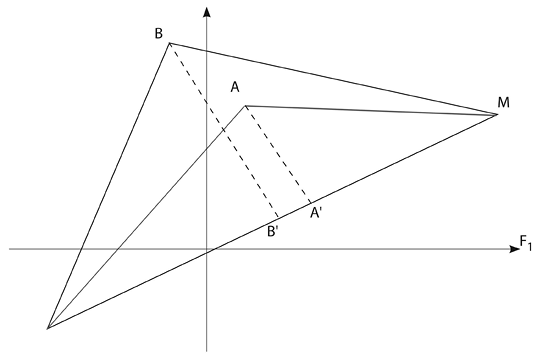
Figure 1. Composite indicator (A, B – municipalities, M, N – accordingly hypothetically best and worst municipalities).
As seen in Fig. 1, the hypothetically worst municipality (N) is given the minimum values of all factors (F1min, F2min, … , Fnmin), while the maximum values of all factors (F1max, F2max, … , Fnmax) go for the hypothetically best municipality. The municipalities will be described accordingly (F1i, F2i, … , Fni). The composite indicator is shown in the picture as a segment B‘N, i.e., the distance from the hypothetically worst municipality (N) to municipality B projected on the segment, which combines the hypothetically best and worst municipalities (MN segment).
According to the Pythagorean Theorem:
BN2 – B'N2=BM2 – B'M2; (6)
BN2 – B'M2=BN2 – B'M2; (7)
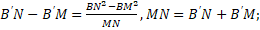 (8)
(8)
 (9)
(9)
Then, we obtain the formula for composite characteristics, which is as follows:
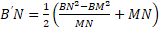 (10)
(10)
The distances BN, BM, and MN are calculated according to the vector distance formula.
First, we calculate the distance of municipality B from the hypothetical worst municipality (distance BN). It is calculated according to the formula:
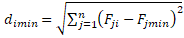 (11)
(11)
Similarly, we calculate the distance between municipality B and the hypothetical best municipality (BM):
 (12)
(12)
The distance from the hypothetical best and worst point (MN) is calculated by the formula:
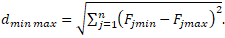 (13)
(13)
Finally, we will find a composite indicator, i.e., the distance from the hypothetical most distant point in the straight line passing through the points, including the hypothetically best and worst municipalities that will allow the evaluation of the rank of each municipality. The final formula for composite characteristics is as follows:
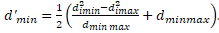 (14)
(14)
4. System of Indicators for the Evaluation of Health Care Institutions
Before analyzing the data, it is essential to discern both the appropriate indicators and those that should not to be included in the analysis. The range of indicators can vary from one to several dozen (Lietuvos 2015). In our case, the indicators were chosen based on the demographic situation, the economic state, the activities and resources of health care institutions, the health status of the population, etc. The feasibility of the selected indicators was further assessed using the Delphi method.
There are 60 municipalities in Lithuania. Most of the doctors are employed in major cities, where medical equipment/facilities are more sofisticated and capable of carrying out extensive research, diagnosing the initial stages of the diseases, locating the focus of these diseases, preventing their spread, or providing appropriate treatment. Smaller towns, due to a lack of medical equipment and experts, can not carry out extensive research and are forced to transfer patients to major cities; case in point, the Vilnius district municipality has signed an agreement that residents of the Vilnius district are serviced by health care institutions in Vilnius. In this way, a better quality of health care services and the coordination of activities are ensured for the residents of the district. Therefore, it is important to that the comparison of the big cities and small towns is carried out as carefully as possible, as the cities differ not only in the structure of their populations but also in the level of how well health care is organized.
After collecting about 50 indicators, we divided them into certain groups:
• Demographic (the distribution of men and women in municipalities, urban population, age, etc.)
• Economic situation (registered unemployment rate in the working age population (15–64));
• Resources (staff of health care institutions, available beds, etc.);
• The performance of health care institutions (visits to doctors);
• The health status of the population (morbidity, mortality, etc.).
In many literature sources, age and gender indicators are closely linked to morbidity and mortality. When analyzing the Lithuanian municipalities, the age indicator is useful in highlighting those municipalities with the highest mortality or morbidity rates. As a result, this indicator can show which municipalities require more health services, e.g., an increased number of nursing/care homes (Car-Hill, Chalmers-Dixon 2005).
The analysis of the age groups according to certain causes of death shows the three main causes of death dominating in Lithuania: external causes of death (110 inhabitants per 100 000 of the population), malignant tumors (287 inhabitants per 100 000 of the population) and diseases of the blood circulatory system (812 inhabitants per 100 000 of the population) (Gaidelytė, Garbuvienė, Madeikytė 2015). It is remarkable that the trends of these causes of death have remained unchanged for some time. In addition, the most common causes of infant mortality are congenital malformation defects, perinatal diseases, and the sudden infant death syndrome. Various sources present data per 100 000 inhabitants, yet there are lower numbers of inhabitants registered in many cities across Lithuania; therefore, a comparison of similar cities or districts or with the average of Lithuania is necessary.
Most data sources provide all health data differentiated based on gender, as inequalities between men and women are common. In Lithuania, life expectancy is increasing, but the difference in life expectancy between men and women remains (69.14 years and 79.63 years, respectively). According to the research, there are a number of factors that can be divided into two groups. The first group can be classified as harmful behaviors that are more common among men, i.e., alcohol consumption, bad eating habits, a risky lifestyle (more likely to be affected by traffic accidents), etc. The second group is more characteristic of women, i.e., individuals prone to health-promoting and reinforcing behavior. In addition, the shorter male life expectancy is determined by the work specifics due to the fact that more men are employed in sectors with needs for physical strength. As a result, the occurrence of additional tension and stress affects health (National Program…, 2015).
The distribution of the population in villages and cities has not changed for a considerable period of time (approximately 2/3 of the Lithuanian population live in cities). The association observed between the place of residence and gender is increasingly more evident. According to a survey conducted by the Social Innovation Fund, urban women are more intensively and frequently concerned about the prevention of specific diseases than men, while in rural areas, they more frequently visit health care institutions not for prophylactic checkups but treatment purposes.
The scientists also see a relationship between an individual’s place of residence, morbidity, and mortality, meaning that one’s place of residence affects their health (Car-Hill, Chalmers-Dixon 2005). According to the data of the Lithuanian Department of Statistics, in 2015, the mortality rate in villages was almost 1.3 times higher than in the cities. It is noticeable that the mortality rate from circulatory diseases in villages (districts) is almost twice higher than in the cities. The main causes of increased mortality are the following: a lack of understanding and awareness among people about the need to take care of their health, a lack of access to health care services (among them prophylactic and preventive), an uneven distribution of health professionals, and shortcomings in the efficient and timely provision, organization and management of health care services. This is especially true for villages that are far from the major cities of Lithuania (The Action Plan…, 2014).
An analysis of the data of the statistical population obtained from the THIF and the data of the OPPHCI show that the largest differences are observed between territories divided into urban and district municipalities, e.g., between the Vilnius city and Vilnius district municipalities. The number of inhabitants who have registered at the OPPHCI in the urban municipalities significantly differs from the numbers provided by the statisticians. Therefore, any calculations of health indicators based on statistical estimates result in statistically significant errors. The largest difference is observed between the Alytus city and district municipalities. The statistical population of Alytus town is 55 614, and the number of registered patients at the OPPHCI exceeds this number by 22 353. Meanwhile, the situation in the Alytus district municipality is different – the statistical population in this territory is 27 126, with only 39% of those registered. The main reason for this discrepancy is internal migration. According to the data of the residents registered at the OPPHCI in Vilnius, the largest number of residents are enrolled during the first months of the academic year, exactly when young people from all over Lithuania arrive to study in the country’s capital.
In 2015, the average number of visits to medical experts (Levels II or III) in Lithuania was 265 per 100 inhabitants. In Vilnius, this indicator was 318 (or 20% higher), in Kaunas – 349 (or 32% higher). In the smaller municipalities of the Skuodas district or Pagėgiai, this indicator did not exceed the average of Lithuania (51%, which is less by 37%). Thus, if this indicator was calculated based on the number of the registered population, even larger discrepancies would occu.
The initial data analysis revealed that the health care indicators are unevenly distributed among the large and small municipalities. Therefore, it was decided to divide the municipalities into two groups and analyze them separately. The smallest municipalities of Neringa and Birštonas were excluded from further analysis due to their specificity. It is also worth noting that due to the low population, the data of these cities and other smaller towns or resorts may be unreliable for making certain conclusions. Thus, this elimination will help to better differentiate the municipalities according to certain health care indicators. The first group consists of the municipalities of the main attraction centers – the largest Lithuanian cities (Vilnius, Kaunas, Šiauliai, Panevėžys, and Šiauliai), district centers (Marijampolė, Mažeikiai, Tauragė, Telšiai, Utena, Alytus), towns with plenty of sanatoriums (Palanga, Druskininkai), and Visaginas. As high indicators were found in these municipalities, it was worth separating them from small municipalities comprising the second group. The municipal data from 2014 were used in the study.
5. Primary Analysis of Statistical Data
At the beginning of the study, a multiple-variable analysis was conducted to find variation coefficients (the ratio between a mean square deviation and an average) separately for municipalities of the main attraction centers and the smaller municipalities in Lithuania. The results of health indicators for both groups under analysis are presented in Table 1. The indicators with a variation coefficient of up to 20% are considered more reliable than those with a higher coefficient of variation. For this reason, part of the indicators had to be eliminated from the principal component and factor analysis models. The analysis of the primary data also takes into account asymmetry and excess coefficients.
When analyzing the larger municipalities, a strong correlation was observed between the following indicators: the number of nurses, the number of dentists, the number of hospital beds, the number of visits to outpatient clinics or ambulatory care units, and the number of doctors. It ranges from 0.80 to 0.93. A strong relationship between these indicators is determined by the “medical services” factor.
Meanwhile, the other group of subjects – the smaller municipalities of Lithuania – shows the only strong correlation (0.78), which is found between the number of doctors and the number of nurses.
Table 2. Coefficient of variation of Lithuanian municipalities (by percent).
|
Health indicators |
Municipalities of the main attraction centers |
Small municipalities |
|
Male (% of total) |
2.7 |
1.9 |
|
Urban population (% of total) |
22.0 |
38.5 |
|
Mortality rate per 1000 of the population |
10.8 |
17.1 |
|
Registered unemployment rate of the working age (15–64) population (%) |
54.0 |
32.6 |
|
Number of doctors with full-time employment status (main job) per 10 000 of the population |
44.8 |
34.7 |
|
Number of nurses with full-time employment status (main job) per 10 000 of the population |
29.7 |
37.3 |
|
Number of dentists with full-time employment status (main job) per 10 000 of the population |
30.8 |
36.5 |
|
Visits to dentists per capita |
24.3 |
30.8 |
|
Visits to doctors per 100 of the population |
11.8 |
9.0 |
|
Number of hospital beds per 10 000 of the population |
36.5 |
34.7 |
|
Hospital morbidity per 1 000 of the poplation |
9.8 |
9.4 |
|
Number of hospitalized patients per day per 1 000 of the population |
27.5 |
29.8 |
|
The average number of visits to outpatient clinics and ambulatory care units per capita |
19.8 |
26.0 |
|
Male median age at the beginning of the year |
5.9 |
5.5 |
|
Number of hospital surgeries per 100 000 of the population |
8.9 |
8.9 |
|
Number of persons provided with emergency medical care per 1000 of the population |
44.4 |
49.2 |
|
Number of pharmacists per 10 000 of the population |
58.1 |
41.2 |
6. Application of Factor Analysis Models
In this study, the principal component method will be used to determine the factors that assume that the principal components are responsible for the total variance of the variables.
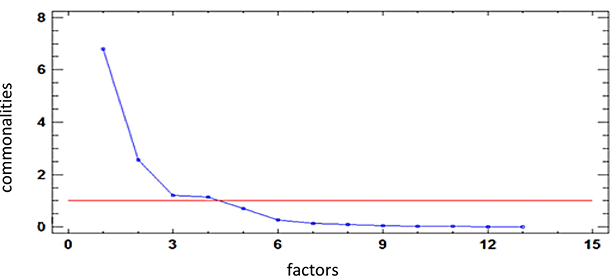
First, we will analyze the first group, i.e., the municipalities of the main attraction centers of Lithuania. Thus, to discover the number of factors that is needed to explain the relationship between the variables, eigenvalues larger than 1 were used in this study. The number of significant factors can also be determined from the graph of eigenvalues.
Figure 2 presents a graph of eigenvalues of the main municipalities in Lithuania. It is obvious that we can distinguish 4 factors that explain 89.99% of the total variance. The remaining factors are irrelevant in this case; their eigenvalues acquire an almost horizontal direction.
Figure 2. The scree plot of eigenvalues of the main attraction centers in Lithuania.
Furthermore, a relationship between the indicators and certain factors is found. However, taking into account the predominance of the first factor, it is difficult to interpret the obtained primary matrix of the factors or to determine which of the variables are related to which factor. To avoid this problem, the factor matrix is rotated. The aim of the rotation is to simplify the matrix structure of the factor weights. This rotation will result in a stronger association between indicators, which will simplify the interpretation of the factors.
Varimax, the most popular orthogonal axis rotation scheme, was chosen in this study. This scheme seeks to ensure that each factor weight for each indicator gets a smaller or higher value. In this way, it is possible to associate each indicator with one particular factor (Pukėnas 2009).
After the rotation is carried out, 4 factors will be examined. The first factor explains most of the variance (52.20%). It is calculated according to the formula:
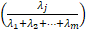 × 100
× 100
The indicators that make up the first factor are worth dividing into two groups: demographic indicators (males of the total % of the population, registered unemployment rate) and the level of medical services (number of doctors, nurses, dentists, and hospital beds). After this distribution of the indicators, the first factor can be called “demography and the level of medical services.”
The demographic indicators will be examined first (first factor). The first indicator of this factor, the proportion of men (in 2014, men accounted for 46.1% of the total population in Lithuania), is negatively affected, which reflects a decrease in the number of men in cities and their emigration to smaller cities and towns. Another group, the level of medical services, reflects the level of employees and institutions in the medical sector. We see that the values of these indicators are high and have a positive impact on the sector of medical services in the main Lithuanian municipalities. These indices are also interrelated in the initial correlation matrix, and their correlation coefficients are quite high. It is worth mentioning that there is an ongoing reorganization of personal health care institutions, as a result of which part of the medical institutions will be closed or merged with larger ones. This is a big issue experienced by regional medical institutions, as they are forced to merge smaller units into larger ones in order to reduce management costs. As a result, a higher level of medical services is transferred to larger cities, which implies that additional staff is needed.
Table 2 . Factors of the main attraction centers in Lithuania.
|
First |
• Male (% of total) (-0.830) • Registered unemployment rate of the working age (15–64) population (0.939) • Number of doctors with full-time employment status per 10 000 of the population (0.864) • Number of nurses with full-time employment status per 10 000 of the population (0.782) • Number of dentists with full-time employment per 10 000 of the population (0.733) • Number of hospital beds per 10 000 of the population (0.859) |
|
Second |
• Urban population (% of total) (0.621) • Mortality rate per 1000 of the population (-0.839) • Visits to doctors per 100 of the population (0.924) |
|
Third |
• Number of hospital patients per day per 1000 of the population (0.662) • Number of hospital surgeries per 100 000 of the population (0.904) |
|
Fourth Male morbidity rate |
• Hospital morbidity per 1000 of the population (0.835) • Male median age (0.905) |
The first factor, the demography and the level of medical services, is more characteristic of large municipalities: the Marijampolė, Mažeikiai, Tauragė, and Telšiai districts, the Visaginas municipality and the municipalities of Lithuania’s largest cities: Kaunas, Klaipėda, Panevėžys, Šiauliai, Vilnius.
The second factor, the activity of the urban population, consists of three indicators that account for 19.71% of the variance. This factor is most strongly influenced by how many visits are payed to doctors.The indicators of the urban population and visits to doctors have a positive loading. Taking into account that these two indicators are quite high, more frequent visits to doctors can also be observed in the future. Meanwhile, the residents living in districts are rarer with their visitors to doctors due to a lack of possibilities or a conservative approach to their health. We can see that the mortality rate correlation coefficients are also high; this component is strongly impacted. Therefore, it has a negative loading. The second factor is dominant in the Alytus city and Utena district municipalities. However, the municipalities of Vilnius city, Telšiai district, and Tauragė district can also be attributed to this factor.
The third factor, hospital services, involves the number of hospital patients and the number of hospital surgeries. It explains 9.37 percent of the variance. Hospital services (third factor) dominate in the Druskininkai municipality. However, if we were to evaluate the municipalities based not only on this factor, several more municipalities (those of the Marijampolė district, Panevėžys city, and Šiauliai city) could be assigned here. Marijampolė distinguished itself from other large municipalities with its smaller number of performed surgeries; however, this number is likely to increase. Due to the closure of the department of obstetrics at the Lazdijai Hospital, patients will be transferred to personal medical care institutions located in Marijampolė or Alytus.
The fourth factor accounts for 8.72% of the variance and consists of two indicators. The values of these indicators are quite high. According to the Lithuanian Department of Statistics, the average life expectancy observed in men of 65 years of age is 5 years shorter than in women (the data for these values from 2014 are, respectively, 79.24 and 84.25 years). This means that men start getting sick earlier; their life expectancy is therefore shorter. In addition, they are frequently affected by harmful habits (alcohol, smoking, drugs, etc.). The Palanga city municipality is dominant in this factor. Compared to other municipalities, it is also characterized by high morbidity. Palanga is known as a sanatorium city, which is why this indicator is high.
Meanwhile, after performing a factor analysis of the data of small municipalities in Lithuania, the model explained a slightly smaller part of the total variance – 71.69%. The first factor explains 37.48% of the variation, the second factor – 12.30%, the third – 11.76%, and the fourth factor – 10.14%.
Table 3. Factors of the small Lithuanian municipalities.
|
First |
• Male (% of total) (-0.637) • Urban population (% of total) (0.783) • Registered unemployment rate of the working age (15–64) population (%) (0.882) • Number of doctors with full-time employment status per 10 000 of the population (0.821) • Number of nurses with full-time employment status per 10 000 of the population (0.676) • Number of hospital beds per 10 000 of the population (0.631) • Visits to doctors per 100 of the population (0.530) • Number of persons provided with emergency medical aid per 1000 of the population (0.505) |
|
Second |
• Male median age (-0.803) • Mortality rate per 1000 of the population (-0.837) • Hospital morbidity per 1000 of the population (0.538) |
|
Third |
• Number of hospital patients per day per 1000 of the population (0.790) • Number of hospital surgeries per 100 000 of the population (0.794) |
|
Fourth |
• Visits to dentists per capita (0.888) |
In major municipalities, population morbidity rates are 1.5 times higher than in small municipalities. According to a study carried out by the Hygiene Institute, up to 16% of hospital patients were hospitalized unnecessarily. In some municipalities, the number of hospital admissions could be reduced, which would help save resources in the health care sector, since hospital cases are the most expensive (Valentienė et al. 2015). An investigation carried out by this institute showed that in the Šilutė district municipality, it was possible to avoid a total of 92.2 cases per 1000 of the inhabitants. The number of hospitalizations that could be avoided was twice lower in municipalities of the Zarasai district, Anykščiai district, Visaginas, Akmenė district, and Kalvarija (Mekšriūnaitė 2014).
The rate of population morbidity in the small Lithuanian municipalities is attributed to the second factor. According to the data of the Hygiene Institute and the data obtained from this study, the municipalities of the Zarasai and Anykščiai districts fall into this factor. These municipalities were more likely to reduce this rate if outpatient care had been better served and better accessible. It was noticed that the opposite concentration of male age was observed among the large and small municipalities of Lithuania. In the future, the mean age of men will increase in the major municipalities of Lithuania, and in the smaller municipalities of Lithuania, on the contrary, the male age will be shorter.
The first factor is dominating in most small municipalities (22), the second factor – in 13, the third factor – in 6, and the fourth factor – in only 3 municipalities.
7. Application of the Principal Component Analysis Methods
The analysis of the principal components of the group of the main Lithuanian attraction centers discloses 4 principal components, which account for 85.26% of the total variance. When analyzing the data, we are interested in only informative principal components, i.e., the principal components with a dispersion larger than 1. Differently from Figure 2, the curve starts to change linearly from 5 but not 4 principal components. However, in order to compare the two methods (factor and principal components), we selected 4 principal components. Therefore, the comparison of these two models would make sense now. In this case, the factor analysis model is better because it explains almost 90% of the total variance, while the principal component model would only explain about 85%. It is worth mentioning that the goals of these two methods are different. The aim of the method of principal components is to explain the distribution of the dispersion, while the factor analysis method aims to explain the correlation of variables.
In terms of the principal component model, the data were standardized – the values of the main components were divided by the corresponding standard deviation. This was performed due to the effect of the relative dispersion of variables on weights. In this case, the dispersions of the variables under analysis are equal. It is noticeable that in both factor and principal component analyses the first two principal factors most commonly account for the most of the total variance. The first factor in this case includes even 8 indicators that describe the level of medical services. This factor explains 51.88% of the total variance. The correlation coefficients for the first principal component are not very high. This means that these indicators have a weak effect on this component. The number of nurses and doctors has the greatest impact. The initial correlation matrix table also shows that most of these indicators are interrelated.
Table 4. Principal components of the main attraction centers in Lithuania.
|
First |
• Male (% of total) (0.264) • Urban population (% of total) (-0.301) • Number of doctors with full-time employment status per 10 000 of the population (-0.321) • Number of nurses with full-time employment status per 10 000 of the population (-0.323) • Number of dentists with full-time employment status per 10 000 of the population (-0.299) • Number of hospital beds per 10 000 of the population (-0.292) • Visits to dentists per capita (-0.290) • Average number of visits to outpatient clinics and ambulatory units per capita (-0.302) |
|
Second |
• Population morbidity per 1000 of the population (0.523) |
|
Third |
• Registered unemployment rate of the working age (15-64) population (%) (0.380) • Mortality rate per 1000 of the population (0.366) • Number of hospital patients per day per 1000 of the population (-0.425) • Number of hospital surgeries per 100 000 of the population (-0.365) • Number of patients with emergency medical services provided per 1000 of the population (0.385) |
|
Fourth |
• Male median age (0.611) • Visits to doctors per 100 of the population (0.483) |
Compared to the first component, the correlation coefficients of the indicators were significantly higher. This indicates the better attribution of the indicators and the effect of a particular factor. If we rate the municipalities under analysis based on this principal component, the best medical services are observed in the municipalities of Kaunas city, the Mažeikiai and Telšiai districts, while the Palanga and Druskininkai municipalities account for the worst medical services.
The second principal component explains 17.75% of the total variance and is formed by only one indicator. This component dominates the municipalities of Palanga and Alytus. These towns are characterized by a large number of rehabilitation and nursing beds. In Palanga, up to 68% of all the beds per 10 000 people were assigned for rehabilitation in 2014, while nursing therapeutic beds dominated in Alytus (there is a sanatorium and a tuberculosis hospital in this town).
The third component includes 5 indicators that account for 8.4% of the variance. These indicators can be divided into two groups: demographic (unemployment rate and mortality indicators) and hospital/emergency services. This component involves the Druskininkai town municipality, which is characterized by high mortality, and the Kaunas city municipality, which has the highest level of unemployment in comparison with other municipalities.
The fourth component is characterized by the indicator of the population’s activity and explains only 7.3% of the total variance. This component dominates in the Visaginas and Vilnius city municipalities. It is obvious that this component is most influenced by the male median age (correlation coefficient 0.611).
The findings obtained from the same study carried out in the small municipalities of Lithuania are presented in Table 5. The data from the small municipalities of Lithuania form the essential 4 principal components, which explain 73.21% of the total variance. The first component explains 39.02% of the variance, the second – 15.29%, the third – 11.47% of the total variance, and the fourth component accounts for 7.43% of the variance.
Table 5. Principal components of the small Lithuanian municipalities
|
First |
• Male (% of total) (0.309) • Urban population (% of total) (-0.277) • Registered unemployment rate of the working age (15–64) population (%) (-0.362) • Number of doctors with full-time employment status per 10 000 of the population (-0.364) • Number of nurses with full-time employment status per 10 000 of the population (-0.370) • Number of hospital beds per 10 000 of the population (-0.329) |
|
Second |
• Visits to doctors per 100 of the population (0.506) • Hospital morbidity per 1000 of the population (-0.367) • Average number of visits to outpatient clinics and ambulatory units per capita (0.488) |
|
Third |
• Mortality per 1000 of the population (-0.435) • Number of hospital patients per day per 1000 of the population (0.568) • Number of hospital surgeries per 100 000 of the population (0.552) |
|
Fourth |
• Male median age (-0.329) • Number of patients with emergency medical services provided per 1000 of the population (0.516) |
The comparison of the results obtained from the small and large Lithuanian municipalities on the basis of the principal component analysis method showed that there were only two indicators (median male age and hospital morbidity) in the large municipalities with a correlation coefficient higher than 0.5, while the correlation between others was weak. Meanwhile, the situation in the small municipalities was slightly different. There were four indicators distinguished there: visits to doctors, the number of hospitalized patients per day, the number of hospital surgeries, and emergency medical services. Figure 5 shows which of the small municipalities dominate in certain principal components.
As the values of the principal components of some municipalities are close, they can be attributed to several areas. The first principal component is dominating in 23 municipalities, the second one – in 8, the third one – in 6, and the fourth one – only in 5 municipalities.
It is evident that the correlation coefficients of the factor analysis variables are higher than those obtained from the principal component method. Therefore, the factor analysis data will be used for a further analysis of the composite municipal indicators.
8. Composite Indicator of Municipalities
We can describe the Lithuanian municipalities of the main attraction centers and the small Lithuanian municipalities using the four already discussed attributes. As the factor analysis indicators in all cases were the highest, we have decided to calculate the composite indicator of the municipalities using the results obtained from factor analysis.
Most of the analyzed main attraction centers demonstrate a quite high level of medical care, especially the big cities – Vilnius, Kaunas, Klaipėda. This situation is slightly different in small towns. Due to a lack of human resources (e.g., ophthalmologists, dentists, internists, surgeons, and other specialists), the residents are forced to go to major cities where they are provided with the necessary services. Only relatively simple operations are carried out in small municipalities, while the patients who require complex surgeries are refered to larger cities. So, in this section, we are interested in analyzing the level of health development in small municipalities (also see Starkienė 2013).
Table 6 presents the values of the composite indicator for the small Lithuanian municipalities. The municipalities with high composite indicator values are more advanced in terms of health care, as they are more distant from the hypothetical worst point. The table shows the relative expression in which the composite indicator is compared to the typical municipality (the typical municipality was determined from the mean values of the respective factors).
Table 6. Composite indicators for municipalities.
|
Municipalities |
Distance from the hypothetically most lagging municipality |
Distance from the hypothetically best performing municipality |
Composite indicator |
Relative expression (%) |
|
Municipalities |
Distance from the hypothetically most lagging municipality |
Distance from the hypothetically best performing municipality |
Composite indicator |
Relative expression (%) |
|
Kaunas distr. m. |
10.986 |
4.056 |
10.446 |
217.57 |
|
Vilnius distr. m. |
10.622 |
3.118 |
10.401 |
216.63 |
|
Alytus distr. m. |
9.858 |
5.292 |
9.060 |
188.70 |
|
Rokiškis distr. m. |
8.063 |
5.259 |
7.803 |
162.53 |
|
Klaipėda distr. m. |
8.344 |
5.706 |
7.791 |
162.27 |
|
Rietavas m. |
8.138 |
6.248 |
7.401 |
154.15 |
|
Pagėgiai m. |
7.489 |
5.570 |
7.317 |
152.40 |
|
Ukmergė distr. m. |
7.378 |
5.828 |
7.136 |
148.63 |
|
Panevėžys distr. m. |
7.448 |
6.035 |
7.080 |
147.45 |
|
Anykščiai distr. m. |
7.463 |
6.796 |
6.703 |
139.60 |
|
Zarasai distr. m. |
7.192 |
6.647 |
6.625 |
137.98 |
|
Biržai distr. m. |
6.685 |
6.345 |
6.502 |
135.42 |
|
Kalvarija m. |
6.913 |
6.762 |
6.409 |
133.48 |
|
Skuodas distr. m. |
6.976 |
6.832 |
6.405 |
133.41 |
|
Kupiškis distr. m. |
6.100 |
6.838 |
5.950 |
123.92 |
|
Akmenė distr. m. |
6.249 |
7.339 |
5.742 |
119.59 |
|
Kėdainiai distr. m. |
6.623 |
7.687 |
5.726 |
119.25 |
|
Varėna distr. m. |
5.831 |
7.410 |
5.501 |
114.57 |
|
Šiauliai distr. m. |
5.485 |
7.599 |
5.234 |
109.01 |
|
Kazlų Rūda m. |
5.506 |
7.935 |
5.037 |
104.91 |
|
Ignalina distr. m. |
5.650 |
8.140 |
4.970 |
103.51 |
|
Jonava distr. m. |
4.791 |
8.168 |
4.598 |
95.76 |
|
Šilalė distr. m. |
4.773 |
8.181 |
4.582 |
95.44 |
|
Jurbarkas distr. m. |
4.739 |
8.177 |
4.572 |
95.23 |
|
Elektrėnai m. |
5.397 |
8.588 |
4.564 |
95.05 |
|
Kaišiadorys distr. m. |
4.630 |
8.263 |
4.476 |
93.22 |
|
Švenčionys distr. m. |
4.278 |
8.644 |
4.098 |
85.35 |
|
Prienai distr. m. |
4.420 |
9.485 |
3.544 |
73.81 |
|
Kelmė distr. m. |
3.718 |
9.251 |
3.491 |
72.72 |
|
Šalčininkai distr. m. |
3.558 |
9.723 |
3.092 |
64.39 |
|
Mažeikiai distr. m. |
3.243 |
9.702 |
3.023 |
62.96 |
|
Raseiniai distr. m. |
3.014 |
10.258 |
2.528 |
52.66 |
|
Trakai distr. m. |
3.347 |
10.428 |
2.473 |
51.51 |
|
Joniškis distr.m. |
2.683 |
10.321 |
2.402 |
50.03 |
|
Plungė distr.m. |
3.329 |
10.543 |
2.373 |
49.42 |
|
Lazdijai distr.m. |
3.716 |
10.750 |
2.306 |
48.03 |
|
Pasvalys distr. m. |
3.049 |
10.713 |
2.159 |
44.97 |
|
Vilkaviškis distr. m. |
3.475 |
10.862 |
2.142 |
44.62 |
|
Kretinga distr. m. |
2.665 |
10.876 |
1.934 |
40.28 |
|
Šilutė distr. m. |
2,509 |
10.873 |
1.905 |
39.67 |
|
Pakruojis distr.m. |
2,003 |
10.820 |
1.860 |
38.73 |
|
Šakiai distr.m. |
3.397 |
11.466 |
1.589 |
33.08 |
|
Radviliškis distr. m. |
1.839 |
11.253 |
1.457 |
30.34 |
|
Širvintos distr. m. |
1.037 |
11.817 |
0.852 |
17.75 |
|
Hypothetically most lagging municipality. |
0.000 |
9.059 |
0.000 |
0.00 |
|
Hypothetically best performing municipality. |
9.059 |
0.000 |
9.059 |
188.67 |
|
Typical municipality. |
5.213 |
8.241 |
4.801 |
100.00 |
Thus, we found that the typical municipality has a value of 4.801. A very close indicator is observed in the municipality of Ignalina districtl therefore, we can assume that this municipality is typical according to the calculations.
Of the 44 small municipalities analyzed, the typical Ignalina municipality ranks in the 21st place, while the health care level of the remaining municipalities is worse. Thus, it is clearly seen that the differences between the smaller municipalities of Lithuania are quite pronounced. The composite indicator of the Širvintos district municipality, which happens to be at the end of the list, is even 12.3 times lower compared to the Kaunas district municipality, which is ranked at the top of the list. The Kaunas district municipality has a very high level of health care development, reaching 218%, while the Širvintos district municipality amounts only up to 18% of the typical level.
The grouping of municipalities was carried out according to the quartile principle. The first quartile comprised eleven best performing municipalities of the districts of Kaunas, Vilnius, Alytus, Rokiškis, Klaipėda, Rietavas, Pagėgiai, Ukmergė, Panevėžys, Anykščiai, and Zarasai, where the highest values of the composite indicator were observed. The third quartile involved eleven lagging municipalities of the districts of Joniškis, Plungė, Lazdijai, Pasvalys, Vilkaviškis, Kretinga, Šilutė, Pakruojis, Šakiai, Radviliškis, and Širvintos with the worst level of medical services. Meanwhile, the remaining 50% of the municipalities were assigned to the group with the median level of medicine.
The municipalities classified as a high medical standard group have a good strategic location and, for this reason, could have reached the top of the list. For example, a number of medical institutions belonging to the municipalities of the districts are actually placed in the cities Vilnius, Kaunas, Klaipėda, and Alytus. As a result, the number of people visiting these health care institutions is growing.
Table 6 shows that the worst medical conditions are observed in the municipalities that fall into the fourth factor. A typical development level of less than 50% is found in the municipalities falling into the fourth factor.
Although the distance was not directly included into the statistical analysis, the research data also clearly demonstrate that the small municipalities located around the big cities most commonly fall into the first group, i.e., the best-performing municipalities in terms of the level of medical care they provide. Meanwhile, low medical level municipalities are found on the border. It is noteworthy that most of the municipalities with a high medical care level are located in the eastern and northeastern regions of Lithuania, while municipalities characterized by poor performance are located in the nothern and western parts of Lithuania.This study confirms that the most lagging municipalities in terms of medical care level are currently located within the largest distance from the main cities of Lithuania.
9. Conclusions
When making an in-depth analysis of data, it is essential to find out the most appropriate indicators. We identified that the most suitable for such research are indicators related to demographic situation, economic state, performance and resources of health care institutions, health status of the population.
Research indicated that most doctors are employed in major cities, where medical facilities are more sofisticated and capable of carrying out extensive research. Smaller towns, due to a lack of medical equipment and medical experts, can not carry out any extensive research and are forced to transfer patients to major cities. In this way, a better quality of health care services and coordination of activities are ensured for the residents of these districts. A careful comparison between the big cities and smaller towns demonstrated that they differ not only in their population structures but also in the level of how well health care is organized. Health care variances in big and small towns are the result of the specificity of the health care sector, which is a major obstacle in making an accurate comparison of health care systems across different municipalities.
Most health indicators in various information systems are calculated by taking into account the number of residents living in municipalities; however, in order to objectively assess the level of inequality among municipalities, it is necessary to calculate the corresponding indicators according to the number of patients who have registered at health care institutions.
Factor analysis and principal components methods were used in this study to clarify and describe the relationship between the health indicators under analysis. Also, the calculation of a composite indicator of municipalities helped to rank these health care institutions based on the level of medical services. By comparing the results obtained on the basis of two multivariate models (factor analysis and principal component analysis), it was found that factor analysis was better and more informative for health care analysis at the regional level.
An analysis of the correlation matrix of the large Lithuanian municipalities indicated a strong correlation between the following indicators: the number of nurses, the number of dentists, the number of hospital beds, the number of visits to outpatient clinics or ambulatory care units, and the number of doctors (from 0.80 to 0.93). In small municipalities, the only strong correlation (0.78) was found between the number of doctors and the number of nurses.
Large cities demonstrate a quite high level of medical care, especially Vilnius, Kaunas, Klaipėda. The situation is different in small towns. Due to the lack of human resources in the health care institutions of these towns, the residents prefer to go to major cities where they are provided with the necessary services. In small municipalities, only relatively simple operations are carried out, and the patients who require complex surgery are refered to larger cities. Small municipalities located around the big cities fall into the group of the best performing municipalities, while the underperforming municipalities are found within the largest distance from the main cities. The values of the composite indicator indicated that the typical Ignalina district municipality ranked in the 21st place. In comparison, the Kaunas district municipality has a very high level of development (218% more than the typical municipality), while the Širvintos district municipality amounts only to 18% of the typical level.
References
The Action Plan for Reducing Health Inequalities in Lithuania for 2014-2023, approved by the Health Minister‘s Order No. V-815 dated of 16 July, 2014.
Car-Hill, R., Chalmers-Dixon, P. (2002). The Public Health Observatory. Handbook of Health Inequalities Measurement. Oxford, Sepho.
Čekanavičius, V., Murauskas, G. (2004). Statistika ir jos taikymai, part 2. Vilnius, TEV, pp. 237–254.
Čepulytė, G., Palubinskienė, S. (2008). Sveikatos draudimo teoriniai aspektai ir finansavimo ypatumai. Lietuvos žemės ūkio universitetas, pp. 131–137.
Čiburienė, J. (2012). Sveikatos apsaugos sektoriaus paslaugų ir gyvenimo kokybės kitimas Lietuvoje. Kauno technologijos universitetas, Lietuva. https://doi.org/10.5755/j01.em.17.4.2998
Dzemyda, G., Kurasova, O., Žilinskas, J. (2008). Daugiamačių duomenų vizualizavimo metodai. Matematikos ir informatikos institutas.
Eidukevičius, R., Juknevičienė, D., Kosareva, N., Pamerneckis, S. (1998). Matematinė statistika istorijoje. Vilnius, Vilniaus universitetas, pp. 190–219.
Gaidelytė, R., Garbuvienė, M., Madeikytė, N. (2015). Lietuvos sveikatos statistika 2015, Lietuvos sveikatos apsaugos ministerija Higienos instituto Sveikatos informacijos centras.
Husson F., L. Pages J. (2010). Exploratory multivariate analysis by example using R. – Chapman and Hall/CRC. Retrieved 14.11.2016 from: http://dx.doi.org/10.1201/b10345.
Lietuvos sveikatos rodiklių sistema Higienos instituto Sveikatos informacijos centras (2015). Retrieved 16.12.2017 from: http://sic.hi.lt/webdps/?lang=lt.
Kėdaitis, V. (1999). Pagrindinių komponenčių analizė. Lietuvos statistikos darbai, t.33.
Kėdaitis, V. (2001). Taikomoji faktorinė analizė. Lietuvos statistikos darbai, t. 39. p. 66–73.
Leiyu Shi (2012). The Impact of Primary Care: A Focused Review. Johns Hopkins Bloomberg School of Public Health, USA. Retrieved 16.12. 2016 from: https://www.hindawi.com/journals/scientifica/2012/432892/.
Lietuvos sveikatos rodiklių sistema. Retrieved 10.11.2015 from: http://www.hi.lt/lt/np-lsris.html.
Mc Killop D., Ferguson Ch. Sibbald A. (2012) An examination of key factors of influence in the development process of credit union industries. Annals of Public and Cooperative Economics, Vol. 73(3), p. 399–428.
Mekšriūnaitė, S. (2014). Visuomenės sveikatos netolygumai. Higienos institutas.
National Programme on Equal Opportunities for Women and Men 2015-2021, Approved by the Government of Lithuania Resolution No 112 of 4 February 2015. Retrieved 15.10.2016 from: https://socmin.lrv.lt/.../documents/files/.../10646_mvlg-programa_en.
Porcelli, F. (2009) Measurement of Technical Efficiency. A Brief Survey on Parametric and Non-Parametric Techniques. P. 27. Retrieved 1.12.2015 from http://www.warwick.ac.uk/fac/soc/economics/staff/phd_students/porcelli/porcelli_dea_sfm.pdf.
Pakėnas K. Kokybinių duomenų analizė spss programa (2009). Lietuvos kūno kultūros akademija. Retrieved 12.12.2017 from: https://www.spssanalize.lt/wp-content/uploads/2014/03/kokybiniu_duomenu_analize_SPSS_programa.pdf.
Starkienė, L. (2013). Netolygus geografinis gydytojų pasiskirstymas: sisteminė kitų šalių patirties apžvalga, Lietuvos sveikatos mokslų universitetas.
Tanna S. (2009). The Impact of Foreign Direct Investment on Total Factor Productivity Growth, Managerial Finance, Vol. 35 Iss 3 p. 297–311. https://doi.org/10.1108/03074350910931799
Valentienė, J., Nedzinskienė, L., Liuima, V., Mekšriūnaitė, S., Sauliūnė, S., Kaselienė, S. Sveikatos netolygumų stebėsena ir vertinimas. Rekomendacijos. Higienos institutas, 2015. Retrieved 20.09.2016 from: http://www.hi.lt/uploads/pdf/projektai/Modelis%20Norway%20Grants/Rekomendacijos.pdf (20.09.2016)
Vaškevičiūtė, D., Kėdaitis, V. (2007). Lietuvos regionų ekonominio-socialinio išsivystymo skirtumų vertinimas daugiamatės analizės metodais. Lietuvos statistikos darbai, Nr. 46, p. 4–41.