Ekonomika ISSN 1392-1258 eISSN 2424-6166
2020, vol. 99(2), pp. 20–38 DOI: https://doi.org/10.15388/Ekon.2020.2.2
Volatility Modeling for Currency Pairs and Stock Indices by Means of Complex Networks
Prof. Olena Liashenko
Taras Shevchenko National University of Kyiv, Ukraine
Email: lyashenko@univ.kiev.ua
Assoc. prof. Tetyana Kravets
Taras Shevchenko National University of Kyiv, Ukraine
Email: tankravets@univ.kiev.ua
Anastasiya Filogina
Taras Shevchenko National University of Kyiv, Ukraine
Email: nastyafilogina@ukr.net
Abstract. Financial markets are complex systems. Network analysis is an innovative method for improving data sharing and knowledge discovery in financial data. Oriented weighted networks were created for the Shanghai Composite, S&P500, DAX30, CAC40, Nikkei225, FTSE100, IBEX35 indexes, for CNY-JPY, EUR-USD, GBP-EUR, RUB-CNY and for cryptocurrency BTC-USD. We considered data since January 6, 2006 to September 6, 2019. The complex networks had a similar structure for both types of markets, which was divided into the central part (core) and the outer one (loops). The emergence of such a structure reflects the fact that, for the most part, the stock and currency markets develop around some significant state of volatility, but occasionally anomalies occur when the states of volatility deviate from the core. Comparing the topology of evolutionary networks and the differences found for the stock and currency markets networks, we can conclude that stock markets are characterized by a greater variety of volatility patterns than currency ones. At the same time, the cryptocurrency market network showed a special mechanism of volatility evolution compared to the currency and stock market networks.
Keywords: complex network, stock index, currency pair, volatility.
Received: 12/05/2020. Revised: 20/06/2020. Accepted: 16/07/2020
Copyright © 2020 Olena Liashenko, Tetyana Kravets, Anastasiya Filogina. Published by Vilnius University Press
This is an Open Access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
1. Introduction
Financial markets, including foreign exchange and stock markets, play an important role in the process of economic growth and development of different countries. Modeling their volatility is important for the financial markets and has not stopped attracting the interest of scientists and practitioners over the last decades.
Uncertainty is inherent in every financial system. This is due to unpredictable behavior of some markets and human psychology. Although the definition of uncertainty in the financial markets may evolve into philosophical discussions, volatility is recognized as a practical measure of risk. Most market variables remain largely unpredictable, but volatility has certain characteristics that can improve its forecasting accuracy. Volatility forecasting has important implications for all risk-adjusted profitability investors. The expected volatility of financial markets is a key variable in financial investment decisions.
Financial markets are complex systems. Network analysis is an innovative method for improving data sharing and knowledge discovery in financial data. In recent decades, complex networks have become a promising area of research. It has applications in many disciplines: statistical physics (Holovatch, Dudka, Blavatska, Palchykov, & Mryglod, 2018), electrical engineering (Saleh, Esa, & Mohamed, 2018), biology (Roy, Grewal, & Roy, 2014), economics (Maluck, Glanemann, & Donner, 2018), climatology (Li, Liu, & Xu, 2017), ecology (Bai, Li, Li, Wang, & Xie, 2016) and sociology (Crossley, 2008). Applications of network theory also include logistic networks, the Internet, social networks and more. The theory of complex networks can be defined as part of the theory of graphs, the birth of which is considered the solution of Leonard Euler known problem of the seven bridges. Further development of the theory was in the works of Rapoport (1957), Watts and Strogatz (1998), Barabási and Albert (1999), Girvan and Newman (2002).
In this article, we are developing the methodology proposed by Liu et al. (2018) to study the dynamics of volatility in stock and currency markets. The database consisted of the Shanghai Composite, S&P500, DAX30, CAC40, Nikkei225, FTSE100, IBEX35 indexes; CNY-JPY, EUR-USD, GBP-EUR, RUB-CNY currency paries and cryptocurrency prices BTC-USD.
Any cryptocurrency differs from classic currencies in form (no paper or physical form) and method of production (mining using complex algorithms). Also, cryptocurrencies are decentralized, i.e. there is no central bank that would control their issuance, but the amount of cryptocurrency (as in the case of bitcoin) issued is limited by certain rules. At the same time, cryptocurrencies can be considered as a commodity (assets) or a security, i.e. as a means of investing and increasing capital. Due to the dual nature of cryptocurrency, it is interesting to explore its properties. The main task that arises is to find out what is closer to the cryptocurrency – security or currency. That is why in our study we compared bitcoin with the dollar (considered a currency pair). As shown by a complex network, the behavior of cryptocurrency is significantly different from the behavior of traditional financial instruments.
The main new element of this article is that it proposes a modified classification algorithm of marking volatility patterns, which is necessary for characterising the greatest volatility of bitcoin.
The purpose of the study is to identify the peculiarities of the stock and currency markets by identifying time series volatility patterns and exploring their evolution. To do this, we use a simulation of the volatility of stock indices and currency pairs using the methods of complex network theory.
The main tasks of the reserch are: comparative analysis of the general characteristics of selected currency and stock markets based on the analysis of indicators of their complex networks; research on evolutionary mechanisms that provide basic information on market volatility; finding out the causes and duration of disturbances (deviations from basic patterns) in the markets; identification of specific evolutionary mechanisms that are indicative of the possible perturbation of the systems.
The article is laid out as follows. After the introduction, Section 2 presents an analysis of recent research. In Section 3, the methodology used is presented with a description of the main complex network techniques as well as the modified classification algorithm of marking volatility paterns. In Section 4, the research results of the methodology application to the stock and currency markets are shown. Finally, Section 5 presents the main conclusions.
2. Analysis of Recent Research
The use of complex network theory for the study of finance and financial markets can be found today in the works of Cao, Li, and Zhang (2017); Moghadam, Mohammadi, Kashani and Shakeri (2019); An, Gao, Guan, Li, and Liu (2016); Gao, Kurths, and Small (2016); Liu, Gao, Fang, Sun, Feng, Liu, and Guo (2018); Gao, An, Fang, Huang, Li, and Zhong (2015). The first group of scholars (Cao et al., 2017) considered the currency market (FX), which is an important part of the financial market. The study aimed to create an international FX network based on complex network theory. The results show that the relationship between exchange rates is tight. According to the study, the US dollar gradually lost its core position, the EUR remained a stable center, and the center of the Asian cluster became unstable.
Iranian researchers Moghadam et al. (2019) became interested in the Tehran Stock Exchange. The results of the analysis of the centrality of the shares indicate that the shares with higher market capitalization, higher risk, higher volume of transactions and less debt ratio (i.e. more liquidity) are more central. These stocks attract more customers due to their attractive investment features and thus have a greater impact on the market.
Among the following groups of researchers should be noted Gao et al. (2015). They concluded that several types of autoregressive patterns cause fluctuations in the financial market. Liu et al. (2018) went further and built a complex network of time series exploring the evolutionary dependence between the models of volatility. In their study, they selected six stock indices as sample data. As a result, all six networks showed a structure of a “petal” consisting of a nucleus and loops, and further scientists described the patterns of evolution and investigated the topological characteristics in networks constructed according to time series, which provided a new perspective for understanding the evolutionary dynamic mechanism.
Aste (2019) studies the dependency and casuality structure of the cryptocurrency market investigating collective movements of both prices and social sentiment related to almost 2000 cryptocurrencies traded during the first six month of 2018. This study introduces several rigorous innovative methodologies applicable to several complex systems where a large number of variables interact in a non-linear way, which is a distinctive feature of the digital economy. The study of cryptocurrencies and more generally of the digital economy require the development of tools beyond traditional approaches with use of instruments from the science of complex systems.
Silva, da Silva, and Tabak (2016) link banking liquidity performance and core-periphery network structures. This work attempts to shed light in the question by analyzing how network topology, in special core-periphery, relates to the banking liquidity performance. By using networks of this structure, effective financial regulation policies can be developed, because central players often score better than peripherals. Networks of this type were tested on data on Brazilian banks.
Guo, Zhang, and Tian (2018) consider stock correlation networks that use stock price data to explore the relationship between different stocks listed in the stock market. There is development of two stock networks using the Minimal Spanning Tree method and study of the topological properties of these networks, including degree, path length and the power-law distribution.
Li and Pi (2018) believe that the global stock market is a typical complex system. This paper uses the complex network method to study the impact of the crisis on the global stock index from 2005 to 2010. For this purpose, three weighted networks are built using a minimum spanning tree. The authors deeply analyze the change of community structure of threshold networks with different thresholds.
Stosic, Stosic, Ludermir, and Stosic (2018) consider the economy as a complex dynamical system. The paper analyzes the cross correlations between the price changes of different cryptocurrencies using random matrix theory methods and the minimum spanning tree.
Tang, Xiong, Jia, and Zhang (2018) systematically examine two major markets for the most influential economies, China and the US, in terms of financial network analysis. In this research, the stock markets are modeled as multiple networks including hierarchical trees, minimum spanning trees, planar maximally filtered graphs, and assets graphs.
Mehtab and Sen (2020) propose a hybrid approach to forecasting stock prices using machine learning and deep learning methods. The study is convincingly aroused by the fact that deep-based learning models have a much higher potential in producing and learning time series data than their corresponding machine learning counterparts.
Pereira, Ferreira, Fernandes, Miranda, and Pereira (2019) analyze the stock exchanges for 20 countries and build a multiscale network identifying the linkages between markets. The results show the central role of European markets among the major global financial markets, mainly France, Germany and the United Kingdom. Similar results were obtained by Wang, Xie, and Stanley (2018). A Pearson correlation network and partial correlation network work were built, that is, two minimally distributed trees (MST-Pearson and MST-Partial) to analyze the correlation structure and evolution of the stock markets.
Rubin, Bassett, and Ready (2019) apply recent innovations in network science to analyze how correlations of stock returns evolve over time. The authors calculate Pearson correlation matrices for each year, and apply multilayer network tools to these correlation matrices to uncover mesoscale architecture in the form of communities.
From all these studies, it follows that the various approaches based on the application of the complex systems methods are actively used to analyze and predict the behavior of financial indicators. In this case, either stock markets, or foreign exchange markets, or the cryptocurrency market are considered separately. In our study, we use the methodology of complex networks for a parallel study of the volatility evolution in all markets in order to identify the characteristics and features of this mechanism.
3. Research Methods
In the theory of complex networks there are three main areas: the study of statistical properties that characterize the behavior of networks; creating a network model; predicting the behavior of networks when changing structural properties. Characteristics of complex networks are generally as follows: large number of nodes; complexity of connections (edges), possible orientation, differentiation of edges weights; nodes and connections between nodes can be generated or lost at any time; some nodes may form compact ensemble groups (Li et al., 2017).
In modern network theory, the number of node connections is called the degree of the node. The notion of degree is a local characteristic of a graph. A non-local, holistic network structure is defined by two concepts: a path and loop. A path is a sequence of adjacent nodes and edges between these nodes when the nodes are not repeated. The loop is the path where the start and end nodes match. Loopless networks are called trees.
For individual nodes, the following parameters are distinguished: input degree of a node – the number of edges of a graph entering a node; output degree of a node – the number of graph edges leaving a node; distance from one node to the other; betweenness centrality, showing how many shortcuts go through a given node.
For the network as a whole, the following characteristics can be distinguished: average weighted degree, network density, average path length, average clustering coefficient, betweenness centrality, dominance of the central node.
In oriented network, the concept of weighted degree of a node can be extended to a degree of inbound 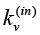 and outbound
and outbound 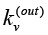 relationships:
relationships:
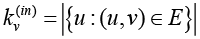 ,
, 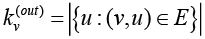 , (1)
, (1)
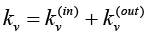 , where E is the set of all edges of the network.
, where E is the set of all edges of the network.
The average weighted degree indicator used in the work is calculated by the following formula:
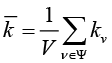 , (2)
, (2)
where Ψ is the set of all nodes of the network, and V is the number of them (Silva & Zhao, 2016).
The distance between nodes is defined as the number of steps that must be taken to get from one node to another through existing edges. Nodes can be connected directly or indirectly through other nodes. The shortest path between the nodes is the minimum distance between them. For the entire network, you can enter the concept of average path length, which is defined as the average of the lengths of the shortest paths taken across all pairs of nodes (Donner, Zou, Donges, Marwan, and Kurths, 2009). Graph density measures how closely connected are the vertices of a graph. It is defined as the proportion of actual connections and the total number of possible connections (Silva & Zhao, 2016).
The clustering coefficient characterizes the tendency to form groups of interconnected nodes. For a particular node, the clustering coefficient characterizes the connection between the neighbors of that node. The ratio of the actual number of connections that connect the closest neighbors of a given node to the maximum possible is the clustering factor of that node. This value does not exceed one.
Betweenness centrality is a parameter that shows how many shortest paths pass through a node. The nodes with the highest mediation play a major role in making connections between other nodes in the network. Thus, assuming that the shortest paths between two vertices are taken, one can determine the importance of the node in terms of its mediation (Costa, Rodrigues, Travieso, and Villas Boas, 2007). The central node dominance is the average difference in mediation between the most central node of the graph and all others. The CPD varies from 0 to 1 and is 0 for all networks where the mediation of all nodes is equal (Freeman, 1977).
For the daily price of the stock index and the currency pair, volatility can be reflected mainly by four elements: the length of the real body, the color of the real body, the length of the upper shadow and the length of the lower shadow. Real body length shows volatility information, which is indicated by the opening price and the closing price. The length of the upper shadow reflects the difference between the highest price and the opening price (or closing price), and the lower shadow considers the difference between the lowest price and the closing price (or opening price). Real body color may indicate the rising (red color) and falling (green color) of indices (Liu et al., 2018).
The body and scale are defined as:
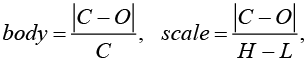 (3)
(3)
where О – open price; C – close price; H – highest price; L – lowest price (Liu et al., 2018; Fock, Klein, and Zwergel, 2005).
A modified classification algorithm was used for the study. This algorithm provided for the introduction of additional states. Body values were divided into 4 intervals: (0, 1%), [1%, 3%], (3%, 7%), [7%, 1). Then, the scale values were distributed into 3 groups: (0, 30%) [30%, 70%] (70%, 1) according to the distribution of the real body. The marking tree for the network is shown in Fig. 1.
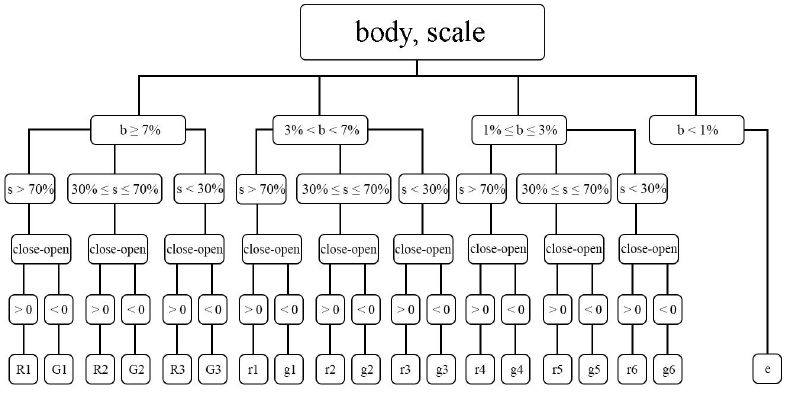
Fig. 1. Marking tree for the network
In order to describe the evolutionary process of volatility patterns, a sliding window was used to divide time series into some segments. According to the fact that the trade is carried out five days a week, the value of the window length was taken at size 5. When setting the step length equal to 1, each subsequent fragment contains 80% of the information of the previous one.
As a result of applying the marking method, the sequence of symbols of daily volatility patterns is matched to the input of the sliding window. After that, the evolutionary process is represented as transitions between the values of sliding windows (volatility patterns), which are in the future considered as nodes of a complex network. The edges of the network represent the evolutionary relationships between the patterns, the weight of the edges is the frequency of evolution between the corresponding patterns.
4. Research results
Oriented weighted networks were created for the Shanghai Composite, S&P500, DAX30, CAC40, Nikkei225, FTSE100, IBEX35 indexes, for CNY-JPY, EUR-USD, GBP-EUR, RUB-CNY and for cryptocurrency BTC-USD. Data was taken (Investing 2019) between January 6, 2006 and September 6, 2019.
For the BTC-USD network, unlike others, there were situations in which the body ≥7% or 3%<body<7% and scale matters at all possible intervals (0,30%), [30%, 70%] and (70%, 1). This indicates greater price volatility during the day than in other currency networks, which is the specificity of a currency such as bitcoin.
Fig. 2 shows that the corresponding networks of these time series demonstrate a petal network structure, and the petals consist of the central part and some outer parts. In addition, all outer parts start from the central part (core), end with the central part and have the form of a loop. Gray circles reflect the size of the primary ‘eeeee’ node in the networks according to their frequency of occurrence. For index networks, these frequencies are 28-42%. The exception is IBEX with a frequency of 23% and Shanghai with 18%. BTC-USD is characterized by the same transitions, but the frequency of appearance of the main node is only 25.5% as opposed to 66–77% in the networks of other currency pairs. The most characteristic pattern of behavior within networks is the transition from the state ‘e’ to ‘g4’, ‘r43’, ‘g5’, ‘r5’ with frequencies of 1-2%. Unlike all other networks considered in the paper, the core of the BTC-USD network consists of nodes containing high volatility states ‘r1’, ‘g1’, ‘R1’ and ‘G1’. It shows the uniqueness of this currency pair, which was manifested in sharp daily price jumps over long periods of time.
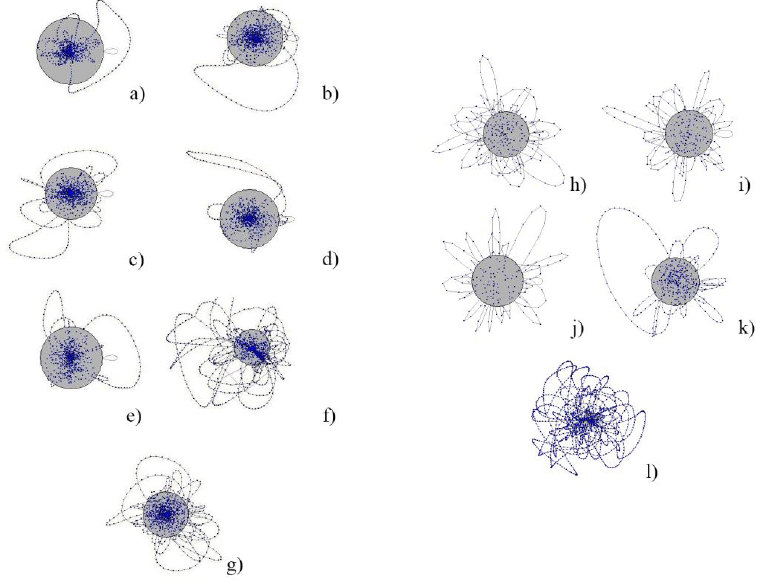
Fig. 2. Stock Index Networks: a) S&P500, b) CAC40, c) DAX30, d) FTSE100, e) Nikkei225, f) Shanghai Composite Index, g) IBEX35; Currency pairs network: h) CNY-JPY, i) EUR-USD, j) GBP-EUR, k) RUB-CNY, l) BTC-USD.
At the next stage of the study, a comparative analysis of the topological indicators of the constructed networks was carried out (Table 1). As can be seen from the table, the number of nodes of the Shanghai Composite network is one and a half times the number of nodes in the other six indices networks. However, for all indexes, the number and complexity of connections between nodes is relatively low (graph density values are only 0.001 for the Shanghai Composite index and 0.002 for all others). The S&P500 has the highest average path length and, accordingly, the highest average evolution efficiency between nodes. At the same time, the IBEX35, DAX30 and CAC40 have the minimal values of the indicators.
The average clustering coefficients of the S&P500 and Nikkei225 are relatively high, indicating that the nodes in these two networks are more closely connected. However, for the FTSE100 the network is comparatively sparse. For the weighted average of the vertices of the seven networks in the S&P500, Nikkei225 and FTSE100, the conversion rate between nodes is much higher, but it is relatively low for the Shanghai Composite and IBEX35 indices. In terms of central point dominance, the lowest is for DAX30 and IBEX35 index networks, the highest is for Nikkei225 and Shanghai Composite.
The information of the topology of currency pairs networks is also presented in Table 1. Note that the number of nodes and complexity of connections between nodes is the lowest for RUB-CNY, the graph is relatively sparse, while the density of the other three networks is from 0.005 to 0.008. The number of nodes and edges in the BTC-USD network is the highest. The average path length is approximately the same in the networks of the three currency pairs (CNY-JPY, EUR-USD and GBP-EUR) and is about 8.5, while in RUB-CNY it is about twice and in BTC-USD it is in seven times. The average clustering factor is the highest in GBP-EUR, which shows that the nodes in this network are more closely connected. However, CNY-JPY and BTC-USD networks are relatively sparse. The average weighted degree of the GBP-EUR is higher than in the other networks. The central point dominates the least in the RUB-CNY network, it is the most dominant in the GBP-EUR network.
Table 1. Components of networks topology of stock indices and currency pairs
|
Nodes |
Edges |
Graph density |
Average path length |
Average clustering coefficient |
Average weighted degree |
Central point |
|
|
S&P500 |
883 |
670 |
0.002 |
21.309 |
0.021 |
5.124 |
0.192 |
|
Shanghai Composite |
1468 |
1105 |
0.001 |
19.315 |
0.016 |
3.007 |
0.219 |
|
Nikkei225 |
833 |
618 |
0.002 |
15.280 |
0.021 |
5.458 |
0.240 |
|
FTSE100 |
963 |
711 |
0.002 |
17.945 |
0.013 |
4.850 |
0.206 |
|
DAX30 |
1081 |
763 |
0.002 |
14.417 |
0.016 |
4.546 |
0.138 |
|
CAC40 |
1149 |
841 |
0.002 |
14.665 |
0.019 |
4.152 |
0.157 |
|
IBEX35 |
1306 |
931 |
0.002 |
13.365 |
0.015 |
3.743 |
0.136 |
|
CNY-JPY |
354 |
261 |
0.0052 |
8.502 |
0.027 |
13.797 |
0.318 |
|
EUR-USD |
341 |
247 |
0.0056 |
8.950 |
0.039 |
14.417 |
0.266 |
|
GBP-EUR |
230 |
170 |
0.0080 |
8.268 |
0.055 |
21.182 |
0.267 |
|
RUB-CNY |
518 |
407 |
0.0031 |
15.286 |
0.036 |
8.848 |
0.235 |
|
BTC-USD |
1720 |
1891 |
0.0006 |
56.009 |
0.015 |
1.600 |
0.251 |
In order to determine the nodes of a complex network core, we consider the statistical characteristics of the weighted degree of nodes. This will reveal the main volatility patterns and the activity of individual volatility patterns in the market.
Fig. 3 presents the curve of the cumulative weighted degree distribution on the basis of the ranked nodes. The curves revealed the inflection points by the tangent method. The nodes lying between the starting point and the inflection point were taken as core nodes. These nodes form the basic structure of the network and the other nodes are loops. It has been found that each network has its own inflection point. In particular, according to the Pareto Principle, basic volatility information for the entire network can be characterized by a small fraction of volatility patterns. That is, in the Chinese stock market, represented by the Shanghai Composite Index, 109 major nodes (9.9% of the total) could display 63.5% of volatility information across the network. In the US stock market, introduced by the S&P500 index, 77.4% of volatility information for the entire market could be reflected by the 57 most common nodes (8.5% of the total). For the German stock market, which could be represented by the DAX30 index, the first 87 nodes (accounting for 11.4% of the total) accounted for 73.7% of the volatility information of the entire network. In addition, volatility information presented at 87 nodes (10.3% of the total) indicated 71.9% of the volatility of the CAC40 index representing the French stock market. For the Japanese stock market, analysis of the Nikkei225 Index Network revealed that 77.0% of volatility information for the entire network could be displayed at 55 major nodes (8.9% of the total). For the UK stock market, the FTSE100 analysis found that the inflection point was (10.6%, 76.4%), indicating that the 75 most important nodes (10.6% of the total) could reflect 76.4% of the volatility of the entire network. The Spanish stock market, represented by the IBEX35, is characterized by a concentration of 70.4% of all volatility information in the main 120 nodes, introducing 12.9% of all nodes.
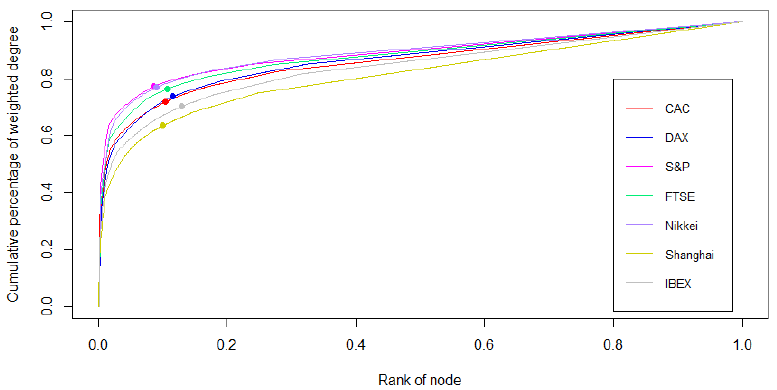
Fig. 3. Cumulative weighted degree distribution of stock indices
From the cumulative weighted degree distribution of currency pairs, it was found that each network had its own inflection point (Fig. 4). In the case of a CNY-JPY 20 node, representing 7.7% of the total, it could display 89.6% of the volatility information of the entire network. In the EUR-USD currency pair, 88.5% of volatility information for the entire market could be indicated by the 16 most common nodes (6.5% of the total). For GBP-EUR, the first 11 nodes (6.5% of total) made up 90.4% of the volatility information of the entire network. When analyzing the RUB-CNY network, it was found that 85.8% of the volatility information of the entire network could be displayed in 21 master nodes (5.2% of the total) in a weighted manner. The situation with the BTC-USD network was unique: only 42.4% of the information was contained in the top 135 nodes (7.8% of the total), which was significantly lower than in other networks.
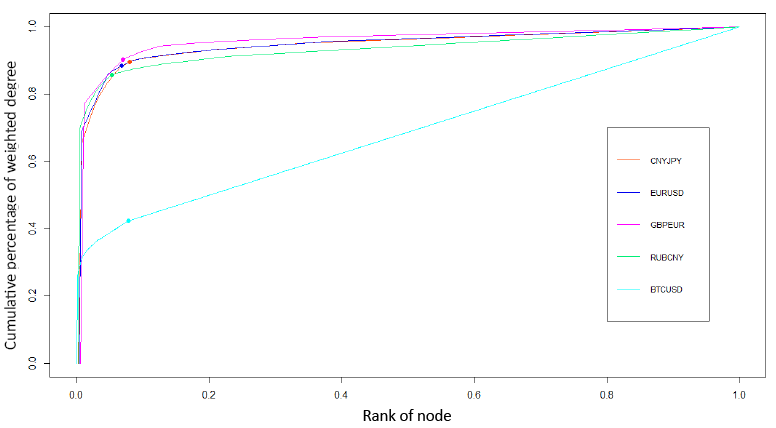
Fig. 4. Cumulative weighted distribution of currency pairs
In order to establish the characteristics of the loops, the nodes in the loops were identified according to the cumulative distribution of the weighted degree. Then the paths of the loops were calculated to analyze the duration of this stock market volatility. It was found (Fig. 5) that for stock indices, most loop lengths were in the range [1, 7], which was about 80% of the total. And almost 15% of the loop lengths were in the range [8, 15]. This statistical result shows that when a stock market enters such a special mode of evolution, it has an 80% probability of ending in a week and a 95% probability of ending in 15 days.
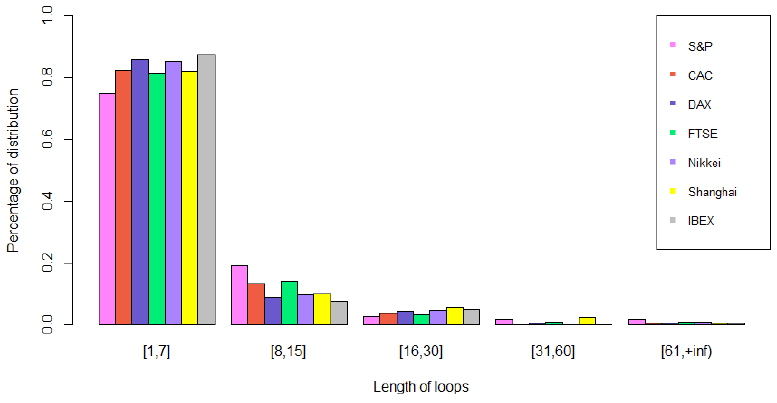
Fig. 5. Probability distribution of stock indices loops
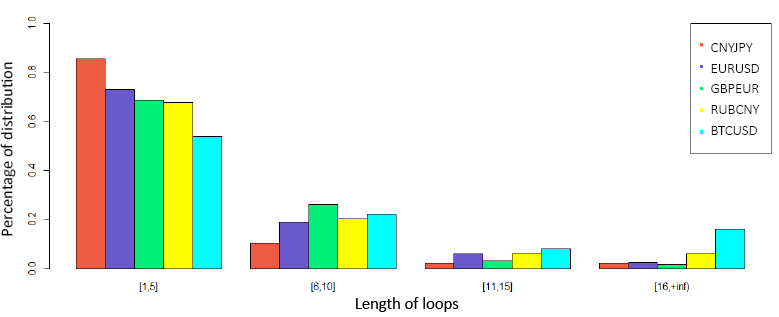
For currency pairs (Fig. 6), most of the loop lengths were in the range [1, 5], which was about 75% of the total. And almost 20% of the loop lengths were in the range [6,10]. This means that the corresponding evolution has a 75% probability of lasting 5 days and a 95% probability of ending within 10 days. However, BTC-USD exhibits excellent behavior, namely: a 5-day loop has a probability of 55%, a duration of up to 10 days is possible with a probability of 77%. Evolution over 16 days is with 18%.
Fig. 6. Probability distribution of currency pairs loops
As for extreme volatility circumstances of more than 60 days in loops, it was found that for the Shanghai Composite, the longest loop was 77 days. In the S&P500 index market, loops lasted for 68 and 86 days. There were the longest loops of 62 days (DAX30), 70 days (CAC40), 64 days (Nikkei225) and 72 days (FTSE100). For currency pairs, the longest loops of 67, 71 and 90 days were in the BTC-USD market. For EUR-USD, they lasted twice for 22 days. GBP-EUR had the longest loop of 34 days and CNY-JPY at 27 days.
It should be noted that the longest loops in all seven indices were in the period September-December 2008. This was due to the bankruptcy of the Lehman Brothers Investment Bank, which filed for bankruptcy in September. The hinges ended in December, when stocks of energy companies rose due to rising oil prices. Immediately after these loops, the S&P500 entered the following long loop in January-April 2009 as interest rates on short-term sovereign debt approach zero. The central bank also announced its intention to tackle deflation through a quantitative easing process. These Fed decisions became the catalyst for the index’s rise in the first quarter of the year. The S&P500 loop, which took place in April-June 2010, was linked to a decline of US stock prices due to fears that the congressional financial reform would curb profits.
The two medium-length hinges of the Shanghai Composite Index in April-July and October-November 2007 were directly related to the sharp rise in this market during the end of 2006–2007. It was driven by the Chinese government‘s efforts to improve the stock market’s efficiency. In addition, the trading environment was optimistic during this period, as economic growth in China and the region was high. The Shanghai Composite loop, due in the winter and spring of 2008, was linked to the US mortgage crisis. The market saw panic sales, causing the market to fall sharply.
The loop of the Shanghai Composite Index, which ran from June to August 2015, had significant prerequisites. Between June 2014 and June 2015, the Shanghai Composite Index rose 150 percent. The main reason for the stock market rally was that many ordinary Chinese people started investing in the stock market for the first time. Retail investors accounted for about 85 percent, they dramatically increased the volatility of the market. Although, on the whole, it was driven by dynamics rather than fundamental indicators. It was in June 2015 that the CSRC announced new terms of margin trading, which became the “last straw.” Stocks seemed highly overvalued at a time when the Chinese economy was losing momentum. The index fallen by almost 30%.
The S&P500, DAX30 and FTSE100 index hinges were in August-October 2011. They were associated with a sharp fall in stock prices on the US, Middle East, Europe and Asia stock exchanges. This was due to concerns about the spread of the sovereign debt crisis in European countries, as well as concerns about the slow economic growth of the United States and a decline in its credit rating.
On the markets of currency pairs, the highest volatility was observed during the end of 2008 - the beginning of 2009. RUB-CNY shown a unique situation in the absence of long loops in crisis years, but their presence at the period from the end of 2014 to 2016.
The turmoil in the CNY-JPY currency market in late 2008 was due to the collapse of the so-called “Kerry Trade” Japanese Yen. Japanese investors were selling risky dollar assets and buying yen. American investors, who borrowed cheaper yen to finance their dollar investment, were faced with rising foreign exchange costs when repaying their loans in yen. They were in a hurry to sell dollars (and other currencies) to buy the yen, which they could use to repay the yen loans, which further increased the yen’s exchange rate. These events have made a significant contribution to the volatility of the currency.
The loop, which took place in the EUR-USD currency pair in October-November 2008, was due to the fact that the US dollar strengthened against the euro after the Italian government announced a significant increase in the target deficit. The size of Italy’s deficit caused concern for investors, as its economy is the third largest in the euro area. The turmoil in the EUR-USD market in April-May 2010 was first conditioned by Greece’s request for EU financial assistance to avoid bankruptcy. Subsequently, fears about the spread of the debt crisis in Europe led to a panic sell-off of the currency, causing a sharp fall in the exchange rate.
The GBP-EUR currency pair loop in January-March 2009 was linked to a fall in sterling as traders pondered the effects of the latest government decision to support the banking sector and the government’s ability to service its debt. The prospect of a prolonged economic downturn and new debt from the British government put a lot of pressure on the sterling, especially after the downgrade of some eurozone countries such as Spain and Greece.
The October 2014 uprising in the RUB-CNY market was driven by a sharp decline in domestic currency inflows from oil exports. Immediately after the end of this hinge, in February 2015, a new, on the contrary, appreciation of the ruble started due to the increase in oil prices, which increased by almost 20% even in two days. Such dynamics were made possible by the fact that US energy companies cut their capital expenditures. In addition, the People’s Bank of China has decided to reduce the minimum reserve requirement for banks since early February, which could stimulate economic activity in the country and demand for energy. The August-September 2015 loop was linked again to the fall in the price of oil and gas, on the one hand, and, on the other, the devaluation of the yuan. All this led to fears that a significant fall in Russia’s exports to China. Coupled with the fact that the ruble fell twice compared to two percent devaluation of the yuan, there was a real prospect of an even more significant collapse of the Russian ruble.
The largest loop in the BTC-USD currency pair, which began in October 2017, was a sharp continuation of the strengthening of bitcoin positions in the market. This was attributed to several reasons. Firstly, some investors were betting that a pair of so-called “hard forks” in one of the base bitcoins that would create two separate versions of cryptocurrency would help boost digital currency assets. Secondly, concerns have been raised that China may grant licenses to exchange digital currencies after the recent ban. The loop ended in January 2018, due to the sharp fall in bitcoin prices. The most popular theory was that asset sales have raised concerns about regulatory action in Asia. The market was flooded with rumors of a total ban on currency in South Korea and a ban on mining in China through heavy electricity consumption. Moreover, it was reported that the Chinese financial authorities planned to block internal access to cryptocurrency trading platforms.
In the next phase of the study, a cumulative distribution of betweenness centrality was applied to find a set of special media nodes in the core structure. These nodes are only used as an intermediate between the loops and the core. It was found that for all indexes there were some nodes (approximately 30% of the total), the cumulative betweenness centrality distribution of which was about 70% of the total. Among the nodes that had a minimum weighted degree in the core, there were some whose values of betweenness centrality in the core and throughout the network were very different. There were several nodes whose centrality was 0 in the core structure, but in the common network these nodes were key media nodes and had relatively high betweenness centrality. The number of such special nodes for the Shanghai Composite and IBEX35 was 16, CAC40 – 9, Nikkei225 and FTSE100 – 8, DAX30 – 6, S&P500 – 3. These nodes were the “end points” of evolution in the core structure, as well as the “start points” of loops. Unlike other media nodes, these nodes only act as bridges between the core and the loops. From a practical point of view, the volatility patterns represented by these nodes are important mechanisms that initiate the transition from standard states (core) to system perturbations (loops). Thus, the emergence of these nodes is a signal of possible disturbances in the stock and currency markets, which are potentially dangerous.
Chronologically entering these nodes for each of the networks can be mapped to one chart with the longest loops. Fig. 7 shows a fragment of the Shanghai Composite Index dynamics with special media nodes applied to it. As the chart shows, there is a tendency for these nodes to coincide with the starting points of the longest loops.
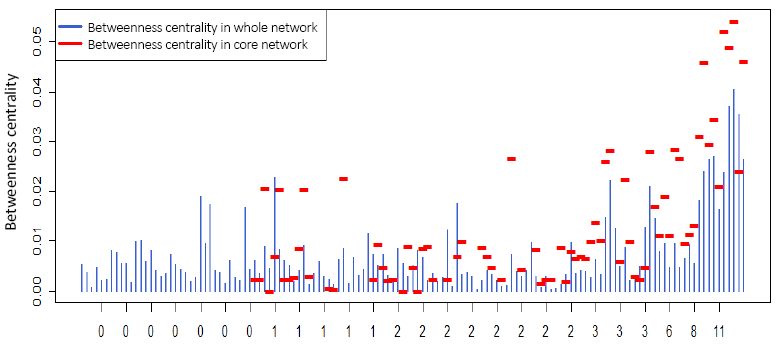
An analysis of the cumulative betweenness centrality distribution revealed that there were also some nodes (about 30% of the total) for currency pairs, whose cumulative mediation is about 60% of the total. Fig. 8 presents a comparison of the betweenness centrality for some nodes in the core and in the whole network for BTC-USD, depending on the weighted degree in core network. The BTC-USD network had 29 special nodes. For the EUR-USD currency pair, there were only 2 such nodes, and for other currency pairs there were no special nodes.
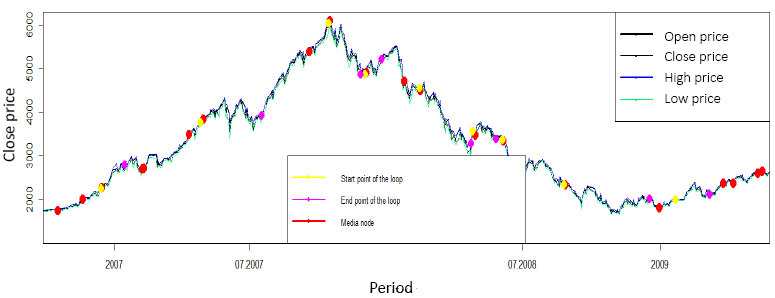
Fig. 7. The fragment of the Shanghai Composite Index dynamics with special media nodes
Fig. 8. Comparison of the nodes mediation in the core and whole network for BTC-USD
Foreign exchange markets, compared to the stock markets, were characterized by a higher degree of the main node, which in turn was an evolutionary ‘eeeee’ pattern. It determines a stable hold within the small gap between the opening and closing prices, which indicates greater stability of these markets in general. In terms of the number of nodes and edges, the density of graphs, stock markets were dominated by foreign exchange markets three times. This speaks to the greater diversification of stock market networks, that is, to the greater number of volatility patterns in them. The average path length in the stock market networks was twice as high as in the foreign exchange markets. This indicates that the evolution to the next pattern in the stock market will take on average twice as long as the foreign exchange market. The average weighted degree was three times higher in the foreign exchange markets, which was related to the already mentioned significantly higher degree of the main node and fewer nodes in general. Central point dominance was also twice or three times higher than in the stock markets. Currency markets, unlike stock markets, had significantly fewer significant volatility patterns. The duration of disturbances in the foreign exchange markets was substantially less than the duration of disturbances in the stock markets. At the same time, the rate of return to the usual patterns of volatility in the foreign exchange market was higher than the stock market. Speaking of special media nodes, the currency markets did not show any tendency for their formation. EUR-USD currency pair alone had two such nodes. For the stock market, the number of special media nodes ranged from 3 to 16.
The BTC-USD network had a somewhat specific nature of the volatility evolution, compared to the networks of the currency and stock markets. By topology, the BTC-USD network was similar to the Shanghai Composite network, but had higher number of nodes, edges, and larger frequencies of the basic node. Graph density was much lower and average path length was much higher in the BTC-USD network compared to all other networks. The process of volatility evolution contained separate high-volatile states inherent only in this network. The BTC-USD network was unique because significant volatility patterns contained one and a half to two times less information than the stock and currency markets. In addition, the duration of the disturbances was significantly higher, and the rates of return to normal volatility patterns were much lower than in other markets. The BTC-USD network had a large number of special media nodes.
Conclusion
The need to analyze a large amount of data has led to the emergence of special methods that are configured to work with big data. Using one of these methods, namely, the theory of complex networks, there was modeled the evolution of the volatility patterns of a group of stock indices and currency pairs.
The complex networks had a similar structure for both types of markets, which was divided into the central part (core) and the outer one (loops). The core consisted of nodes that had a higher weighted degree in the network, and the other nodes formed loops. In addition, all the loops started from the central part and ended there. The emergence of such a structure reflects the fact that, for the most part, the stock and currency markets develop around some significant state of volatility, but occasionally anomalies occur when the states of volatility deviate from the core.
Technical modeling tools were accompanied by a fundamental analysis in which quantitative information was used in conjunction with macroeconomic information. This approach helped to find out the causes of the greatest disturbances found in the markets, i.e. the medium and long loop outputs. The longest of these occurred in the fall of 2008. If we talk about the general trend, most of the long disturbances occurred precisely on the declining trends of indicators, which is easily explained by behavioral factors of influence, in particular the panic of traders.
In the course of the study, specific volatility patterns were highlighted, which only occured in the event of market turmoil. Such nodes had a high level of mediation in the network structure, whereas in the core structure their level of mediation was zero. The transition to such nodes is a prerequisite for disturbances in the relevant market.
Comparing the topology of evolutionary networks and the differences found for the stock and currency markets networks, we can conclude that stock markets are characterized by a greater variety of volatility patterns than currency ones. At the same time, the cryptocurrency market network showed a special mechanism of volatility evolution compared to the currency and stock market networks. As can be seen from our research, bitcoin has nothing to do with ordinary currencies (in particular, the dollar) and it behaves completely differently in terms of the reaction of its exchange rate to the processes taking place in the currency market.
References
An, F., Gao, X., Guan, J., Li, H., & Liu, Q. (2016). An evolution analysis of executive-based listed company relationships using complex networks. Physica A: Statistical Mechanics and its Applications, 447, 276–285. http://doi.org/10.1016/j.physa.2015.12.050.
Aste, T. (2019). Cryptocurrency market structure: connecting emotions and economics. Digital Finance, 1, 5-21. http://doi.org/10.1007/s42521-019-00008-9.
Bai, Y., Li, C., Li, Y., Wang, X., & Xie, J. (2016). Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions. Atmospheric Pollution Research, 7, 557–566. http://doi.org/10.1016/j.apr.2016.01.004.
Barabási, A.-L., & Albert, R. (1999). Emergence of Scaling in Random Networks. Science, 286, 509–512 (1999). http://doi.org/10.1126/science.286.5439.509.
Cao, G., Li, Q., & Zhang, Q. (2017). Causal relationship between the global foreign exchange market based on complex networks and entropy theory. Chaos, Solitons & Fractals, 99, 36–44. http://doi.org/10.1016/j.chaos.2017.03.039.
Costa, L.F., Rodrigues, F.A., Travieso, G., & Villas Boas, P.R. (2007). Characterization of complex networks: A survey of measurements. Advances in Physics, 56, 167–242. http://doi.org/10.1080/00018730601170527.
Crossley, N. (2008). Small-World Networks, Complex Systems and Sociology. Sociology, 42, 261–277. http://doi.org/10.1177/0038038507087353.
Donner, R.V., Zou, Y., Donges, J.F., Marwan, N., & Kurths, J. (2009). Recurrence network – A novel paradigm for nonlinear time series analysis. New Journal of Physics, 12(3). DOI:10.1088/1367-2630/12/3/033025.
Fock, J.H., Klein, C., & Zwergel, B. (2005). Performance of Candlestick Analysis on Intraday Futures Data. The Journal of Derivatives, 13, 28–40. http://doi.org/10.3905/jod.2005.580514.
Freeman, L.C. (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry, 40(1), 35-41. http://doi.org/10.2307/3033543.
Gao, X., An, H., Fang, W., Huang, X., Li, H., & Zhong, W. (2015). Characteristics of the transmission of autoregressive sub-patterns in financial time series. Scientific Reports 4, 6290. http://doi.org/10.1038/srep06290.
Gao, Z.-K., Kurths, J., & Small, M. (2016). Complex network analysis of time series. EPL (Europhysics Letters), 116, 50001. http://doi.org/10.1209/0295-5075/116/50001.
Girvan, M., & Newman, M.E.J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99, 7821–7826. http://doi.org/10.1073/pnas.122653799.
Guo, X., Zhang, H., & Tian, T. (2018). Development of stock correlation networks using mutual information and financial big data. PLoS One, 13(4): e0195941. http://doi.org/10.1371/journal.pone.0195941.
Holovatch, Y., Dudka, M., Blavatska, V., Palchykov, V., Krasnytska, M., & Mryglod, O. (2018). Statistical physics of complex systems in the world and in Lviv. Journal of Physical Studies, 22(2), 2801(21p.). http://doi.org/10.30970/jps.22.2801.
Li, B., & Pi, D. (2018). Analysis of global stock index data during crisis period via complex network approach. PLoS One, 13(7): e0200600. http://doi.org/10.1371/journal.pone.0200600.
Li, W., Liu, Z., & Xu, J. (2017). Complex network analysis of climate change in the Tarim River Basin, Northwest China. Sciences in Cold and Arid Regions, 9(5), 476-487. http://www.scar.ac.cn/EN/10.3724/SP.J.1226.2017.00476.
Liu, S., Gao, X., Fang, W., Sun, Q., Feng, S., Liu, X., & Guo, S. (2018). Modeling the Complex Network of Multidimensional Information Time Series to Characterize the Volatility Pattern Evolution. IEEE Access, 6, 29088–29097. http://doi.org/10.1109/access.2018.2842069.
Maluck, J., Glanemann, N., & Donner, R.V. (2018). Bilateral Trade Agreements and the Interconnectedness of Global Trade. Frontiers in Physics, 6. http://doi.org/10.3389/fphy.2018.00134.
Mehtab, S., & Sen, J. (2020). Stock ptice prediction using convolutional neural networks on a multivariate time series. arXiv: 2001.09769.
Moghadam, H.E., Mohammadi, T., Kashani, M.F., & Shakeri, A. (2019). Complex networks analysis in Iran stock market: The application of centrality. Physica A: Statistical Mechanics and its Applications, 531, 121800. http://doi.org/10.1016/j.physa.2019.121800.
Pereira, E.J., Ferreira, P.J.C., Fernandes, M., & Pereira, H.B.B. (2019). Multiscale network for 20 stock markets using DCCA. Physica A: Statistical Mechanics and its Applications, 529, 121542. https://doi.org/10.1016/j.physa.2019.121542.
Rapoport, A. (1957). Contribution to the theory of random and biased nets. The Bulletin of Mathematical Biophysics, 19, 257–277. http://doi.org/10.1007/bf02478417.
Roy, U., Grewal, R.K., & Roy, S. (2014). Complex Networks and Systems Biology. In: Systems and Synthetic Biology. Springer Netherlands, pp. 129–150. http://doi.org/10.1007/978-94-017-9514-2_7.
Rubin, D.N., Bassett, D.S., & Ready, R. (2019). Uncovering dynamic stock return correlations with multilayer network analysis. Appl. Netw. Sci. 4, 31. https://doi.org/10.1007/s41109-019-0132-5.
Saleh, M., Esa, Y., & Mohamed, A. (2018). Applications of Complex Network Analysis in Electric Power Systems. Energies, 11, 1381. http://doi.org/10.3390/en11061381.
Silva, T.C., Soares da Silva, M., & Tabak, B.M. (2016). Financial networks and bank liquidity. Journal of Network Theory in Finance, 2(4), 1-51. http://doi.org/10.21314/JNTF.2016.022.
Silva, T.C., & Zhao, L. (2016). Machine Learning in Complex Networks. Springer International Publishing. http://doi.org/10.1007/978-3-319-17290-3.
Stosic, D., Stosic, D., Ludermir, T.B., & Stosic, T. (2018). Collective behavior of cryptocurrency price changes. Physica A: Statistical Mechanics and its Applications, 507, 499-509. https://doi.org/10.1016/j.physa.2018.05.050.
Tang, Y., Xiong, J.J., Jia, Z.Y., & Zhang, Y.C. (2018). Complexities in financial network topological dynamics: modeling of emerging and developed stock market. Complexity. http://doi.org/10.1155/2018/4680140.
Wang, G., Xie, C., & Stanley, H.E. (2018). Correlation structure and evolution of world stock markets: evidence from Pearson and partial correlation-based networks. Comput. Econ. 51, 607-635. https://doi.org/10.1007/s10614-016-9627-7.
Watts, D., & Strogatz, S. (1998). Collective dynamics of “small-world” networks. Nature, 393, 440–442. http://doi.org/10.1038/30918.