Elipsinių kreivių L funkcijų diskrečiojo universalumo tyrimas

The Investigation of the Discrete Universality of L-Functions of Elliptic Curves

Samanta Zakaitė
samanta.zakait@gmail.com

Antanas Garbaliauskas
Šiaulių valstybinė kolegija
a.garbaliauskas@svako.lt

Santrauka. Darbe įrodyta elipsinių kreivių L funkcijų diskrečiojo universalumo teorema silpnojo tikimybinių matų konvergavimo prasme analizinių funkcijų erdvėje. Nagrinėjamas analizinės funkcijos aproksimavimas postūmiais , čia m įgyja reikšmes iš diskrečiosios aibės, pavyzdžiui, aritmetinės progresijos. Fiksuotas skaičius h > 0 pasirenkamas taip, kad exp{2πk/h} būtų racionalusis skaičius su tam tikrais . Elipsinių kreivių L funkcijų diskrečiojo universalumo įrodymas remiasi šios funkcijos diskrečiąja ribine teorema tikimybinių matų silpnojo konvergavimo prasme analizinių funkcijų erdvėje.

Reikšminiai žodžiai: elipsinių kreivių L funkcija, ribinė teorema, diskretusis universalumas.

Summary. In the paper, we prove the discrete universality theorem in the sense of the weak convergence of probability measures in the space of analytic functions for the L-functions of elliptic curves. We consider an approximation of analytic functions by translations , where h > 0 is a fixed number, m takes values from some discrete set such as arithmetical progression. We suppose that the number h > 0 is chosen so that exp{2πk/h } is a rational number for some . The proof of discrete universality of L-functions of elliptic curves is based on a limit theorem in the sense of weak convergence of probability measures in the space of analytic functions.

Keywords: L-function of elliptic curves, limit theorem, discrete universality.

Received: 2022-05-02. Accepted: 2022-05-23
Copyright © 2022 Samanta Zakaitė, Antanas Garbaliauskas. Published by Vilnius University Press. This is an Open Access article distributed under the terms of the Creative Commons Attribution Licence, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Įvadas

Tegul E elipsinė kreivė virš racionaliųjų skaičių kūno duota Vejerštraso (Weierstrass) lygtimi

, Z.

Pažymėkime kreivės E diskriminantą. Tada kubinio trinario šaknys yra skirtingos ir kreivė E yra nesinguliarioji.

Kiekvienam pirminiam p pažymėkime lyginio

sprendinių skaičių. Tegu o – kompleksinis kintamasis. Tuomet elipsinės kreivės L funkcija apibrėžiama Oilerio (Euler) sandauga

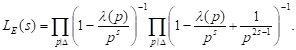
Remiantis Hasės (Hasse) įverčiu

begalinė sandauga, apibrėžianti funkciją , konverguoja absoliučiai ir tolygiai pusplokštumės kompaktiniuose poaibiuose ir apibrėžia analizinę nelygią nuliui funkciją. Šioje srityje funkcija gali būti išreikšta Dirichlė (Dirichlet) eilute

čia yra multiplikatyvioji funkcija, o ši eilutė taip pat absoliučiai konverguoja srityje .

Funkcijos analizinis pratęsimas glaudžiai susijęs su tam tikrų modulinių formų L funkcijomis. Funkcijos analizinės savybės sutampa su svorio 2 naujųjų formų L funkcijų savybėmis.

1 savybė. Funkcija analiziškai pratęsiama į visą kompleksinę plokštumą ir tenkina funkcinę lygtį

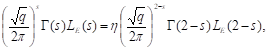
čia q – natūralusis skaičius, sudarytas iš diskriminanto pirminių daugiklių, , o yra Oilerio gama funkcija.

2 savybė. Furjė eilutė

yra svorio 2 naujoji forma kurio nors Hekės pogrupio atžvilgiu.

Šias savybes 2001 metais įrodė C. Brioilis (Breuil), B. Konradas (Conrad), F. Daimondas (Diamond) ir R. Teiloras (Taylor) [2].

Elipsinių kreivių L funkcija, kaip ir dauguma klasikinių dzeta ir L funkcijų, yra universali Voronino prasme. Liniko-Ibragimovo hipotezė sako, kad visos funkcijos tam tikroje pusplokštumėje apibrėžtos Dirichlė eilute, analiziškai pratęsiamos į kairę nuo absoliutaus konvergavimo pusplokštumės ir tenkinančios tam tikras didėjimo sąlygas, yra universalios Voronino prasme.

Rymano ir L funkcijų universalumas plačiai taikomas kvantinėje mechanikoje, kondensuotų medžiagų fizikoje bei statistinėje fizikoje [6].

Pažymėkime meas A mačiosios aibės Lebego matą. Kai , tegul

čia vietoj daugtaškio įrašomos sąlygos, kurias tenkina . Tegul žymi kompleksinę plokštumą, o sritis . Tolydaus tipo universalumo teoremą elipsinių kreivių L funkcijai įrodė A. Laurinčikas ir V. Garbaliauskienė.

A teorema [4]. Tarkime, kad E yra nesinguliarioji elipsinė kreivė virš racionaliųjų skaičių kūno. Tegul K yra juostos D kompaktinis poaibis su jungiuoju papildiniu, o yra tolydi nelygi nuliui funkcija poaibyje K ir analizinė K viduje. Tuomet su kiekvienu ε >0

Pastaroji teorema rodo, kad egzistuoja be galo daug postūmių , kurie norimu tikslumu ε aproksimuoja duotąją analizinę funkciją . Be to aibė tokių turi teigiamą apatinį tankį. Tolydaus tipo universalumo teoremose kinta tolydžiai intervale [0, T].

Be šio tipo teoremų egzistuoja universalumo teoremų diskretusis atvejis. Rymano dzeta funkcijos diskretųjį universalumą nagrinėjo S. M. Voroninas (Voronin) (1979) [9] ir B. Bagči (Bagchi) (1981) [1] . Šio universalumo atveju postūmio menamoji dalis įgyja reikšmes iš tam tikros diskrečiosios aibės, pavyzdžiui, iš aritmetinės progresijos. Tegu ir

čia vietoj daugtaškių įrašomos sąlygos, kurias tenkina m, o yra fiksuotas skaičius.

Elipsinių kreivių L funkcijų diskretųjį universalumą įrodė V. Garbaliauskienė ir A. Laurinčikas.

B teorema ([3]). Tarkime, kad yra iracionalusis skaičius su visais . Tegul K yra juostos D kompaktinis poaibis su jungiuoju papildiniu, o yra tolydi nelygi nuliui funkcija poaibyje K ir analizinė K viduje. Tuomet su kiekvienu ε >0

Šioje teoremoje matome, jog postūmių , aproksimuojančių duotąją analizinę funkciją, aibė yra pakankamai gausi: ji turi teigiamą apatinį tankį.

Atvejis, kai yra racionalusis skaičius, su kuriais nors yra sudėtingesnis. Sudėtingumo problemos kyla iš ribinės teoremos analizinių funkcijų erdvėje funkcijai .

Šio straipsnio tikslas – įrodyti elipsinių kreivių L funkcijų diskretųjį universalumą, pasirenkant tokį, kad būtų racionalusis skaičius tam tikriems .

1 teorema. Tarkime, kad egzistuoja sveikasis skaičius , toks, kad yra racionalusis skaičius. Tegu K yra juostos D kompaktinis poaibis su jungiuoju papildiniu, o yra tolydi nelygi nuliui funkcija poaibyje K ir analizinė K viduje. Tuomet su kiekvienu ε >0

Teoremos įrodymas remiasi diskrečiosiomis ribinėmis teoremomis tikimybinio mato silpnojo konvergavimo prasme.

Diskrečioji ribinė teorema funkcijai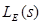

Pirmiausiai apibrėšime atsitiktinį elementą analizinių funkcijų erdvėje. Kadangi yra racionalusis skaičius su tam tikrais sveikaisiais , todėl pakanka pasirinkti tik teigiamuosius skaičius k, tenkinančius šią savybę. Tegul yra mažiausias iš jų. Tada kiti skaičiai yra skaičiaus kartotiniai [7]. Tarkime, kad

Tegul yra vienetinis apskritimas kompleksinėje plokštumoje . Apibrėžkime begaliniamatį torą

,

čia su kiekvienu pirminiu p. Su sandaugos topologija ir pataškine daugyba yra kompaktinė tolopoginė Abelio (Abelian) grupė. Pažymėkime elemento projekciją koordinatinėje erdvėje su visais tegul

čia reiškia, kad , bet . Dėl to, yra visiškai multiplikatyvi funkcija ir

Pažymėkime – metrinės erdvės S Borelio (Borel) aibių klasę, o H(D) – analizinių srityje D funkcijų erdvę su tolygaus konvergavimo kompaktuose topologija. Apibrėžkime

Tuomet yra toro uždarasis pogrupis, todėl jis taip pat yra kompaktinė topologinė Abelio grupė. Tokiu būdu erdvėje galime apibrėžti tikimybinį Haro (Haar) matą . Taip gauname tikimybinę erdvę .

Tegul kompleksinės plokštumos sritis, o su visais ir ,

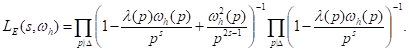
2 teorema. yra reikšmis atsitiktinis elementas, apibrėžtas tikimybinėje erdvėje .

Įrodymas. Erdvėje apibrėžtas tikimybinis Haro matas . Tegul yra pasirenkama baigtinė pirminių skaičių aibė, . Pasinaudosime [7] darbe sukonstruota mačiąja funkcija . Pažymėkime funkcijos siaurinį koordinatinėje erdvėje . Kadangi yra nepriklausomų atsitiktinių elementų, apibrėžtų tikimybinėje erdvėje , seka ir gauname

Vadinasi, yra nepriklausomų atsitiktinių elementų, apibrėžtų tikimybinėje erdvėje , seka.

Teoremai įrodyti pakanka parodyti, kad sandauga

beveik tikrai tolygiai konverguoja srities kompaktiniuose poaibiuose. Tam pakanka įrodyti, kad srities kompaktiniuose poaibiuose beveik tikrai konverguoja eilutė

(1)

čia

Atsitiktinio elemento vidurkį pažymėkime . Aišku, kad

todėl su kiekvienu pirminiu . Be to,

Remiantis Hasės įverčiu gauname, kad

su visais Kadangi yra nepriklausomų atsitiktinių dydžių seka ir eilutės

ir

konverguoja, pagal jau žinomą 1.2.11 teoremą iš [8], gauname, kad eilutė (1) konverguoja beveik tikrai kiekvienam fiksuotam Tačiau (1) yra Dirichlė eilutė, kuri tolygiai konverguoja srities kompaktiniuose poaibiuose su beveik visais mato atžvilgiu. Teorema įrodyta.

Suformuluosime ribinę teoremą elipsinių kreivių L funkcijai analizinių funkcijų erdvėje.

3 teorema. Tarkime, kad egzistuoja sveikasis skaičius ir fiksuotas , tokie, kad būtų racionalusis skaičius. Tada tikimybinis matas

silpnai konverguoja į atsitiktinio elemento skirstinį, kai

Universalumo teoremos įrodymas remiasi diskrečiąja ribine teorema analizinių funkcijų erdvėje. Pastarajai teoremai įrodyti naudojamos ribinės teoremos Dirichlė polinomams bei ribinės teoremos absoliučiai konverguojančioms Dirichlė eilutėms [5].

Atsitiktinio elemento 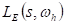atrama

Tegul yra laisvai pasirenkamas skaičius, toks, kad Aišku, kad , todėl taip pat yra -reikšmis atsitiktinis elementas, apibrėžtas tikimybinėje erdvėje . Pažymėkime jo skirstinį .

Norint įrodyti universalumo teoremą, mums reikės -reikšmio atsitiktinio elemento skirstinio atramos juostoje Priminsime, kad mato Q atrama yra vadinama tokia minimali uždara aibė , kad Aibė yra sudaryta iš tokių elementų kurių bet kuriai atvirai aplinkai G yra teisinga nelygybė .

Tegul , ir

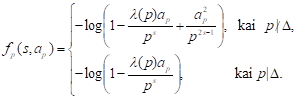(2)

4 lema [3]. Visų konverguojančių eilučių

aibė erdvėje yra tirštoji aibė.

Dabar esame pasirengę apibrėžti atramą. Tegul

.

5 lema. -reikšmio atsitiktinio elemento skirstinio atrama yra aibė .

Įrodymas. 2 teoremos įrodyme gauta, kad yra nepriklausomų atsitiktinių dydžių, apibrėžtų tikimybinėje erdvėje , seka. Todėl, išlaikydami (2) žymėjimą, turime, kad yra erdvės nepriklausomų -reikšmių atsitiktinių elementų seka. Atsitiktinio elemento atrama yra aibė

.

Vadinasi, remiantis 1.7.10 teorema iš [8], -reikšmio atsitiktinio elemento

atrama yra visų konverguojančių eilučių

aibės uždarinys. Remiantis 4 lema, pastaroji aibė yra tiršta erdvėje . Pažymėkime funkciją, apibrėžtą formule , . Ši funkcija priskirianti ir priskirianti yra tolydi. Taigi, atrama apima . Tačiau atrama yra uždara aibė. Todėl, remiantis Hurvico (Hurwitz) teorema (žr. [8], 6.5.5 lema), . Tokiu būdu atrama apima . Kita vertus, beveik tikrai konverguojanti nenulinių daugiklių sandauga, vadinasi, pagal tą pačią Hurvico teoremą, atrama beveik tikrai priklauso . Lema įrodyta.

1 teoremos įrodymas

Pasirenkame tokį, kad . Tarkime, kad turi nenulinį analizinį pratęsimą į sritį . Apibrėžkime atvirąją aibę G formule

Iš 5 lemos seka, kad , o iš 3 teoremos gauname, kad

(3)

Tegul tenkina 1 teoremos sąlygas. Tada pagal Mergeliano teoremą [10] srities kompaktiniame poaibyje K egzistuoja daugianaris , , toks, kad

(4)

Taip pat egzistuoja daugianaris toks, kad

Iš šios ir (4) nelygybių matome, kad

(5)

Kadangi , iš (3) randame, kad

Iš šios ir (5) nelygybės gauname teoremos tvirtinimą.

Išvados

1. Elipsinių kreivių L funkcijai galioja diskrečioji ribinė teorema tikimybinių matų silpnojo konvergavimo prasme analizinių funkcijų erdvėje.

2. Funkcijai galioja diskrečiojo universalumo nelygybė, kai yra racionalusis skaičius su tam tikrais .